스케줄링 문제를 풀 때 자주 등장하는 기법으로 Constraint Programming(CP)이 있다.
이번에는 CP가 정확히 어떤 것 인지 알아보고자 다음 논문을 읽어보았다.
논문의 제목은 A hybrid Constraint Programming/Mixed Integer Programming framework for the preventive signaling maintenance crew scheduling problem이며,
논문에서는 스케줄링 문제에 CP와 MIP(Mixed Integer Programming)를 활용한 방법을 제시한다.
주제
아 논문에서는 덴마크의 철도 신호장치(railway signaling system) 유지, 보수 팀에 대한 스케줄링을 주제로 한다.
특히, 현실적인 제약을 많이 고려하고 있다. 예를 들어, 하루 이상 걸리는 작업을 쪼갠다던가, crew들의 능력을 고려하여 일정을 짠다던가하는 제약들이 있다.
논문에서는 이러한 문제를 풀기 위해 CP로 초기해를 만들고, 이를 MIP를 통해 개선하는 방법을 제시한다.
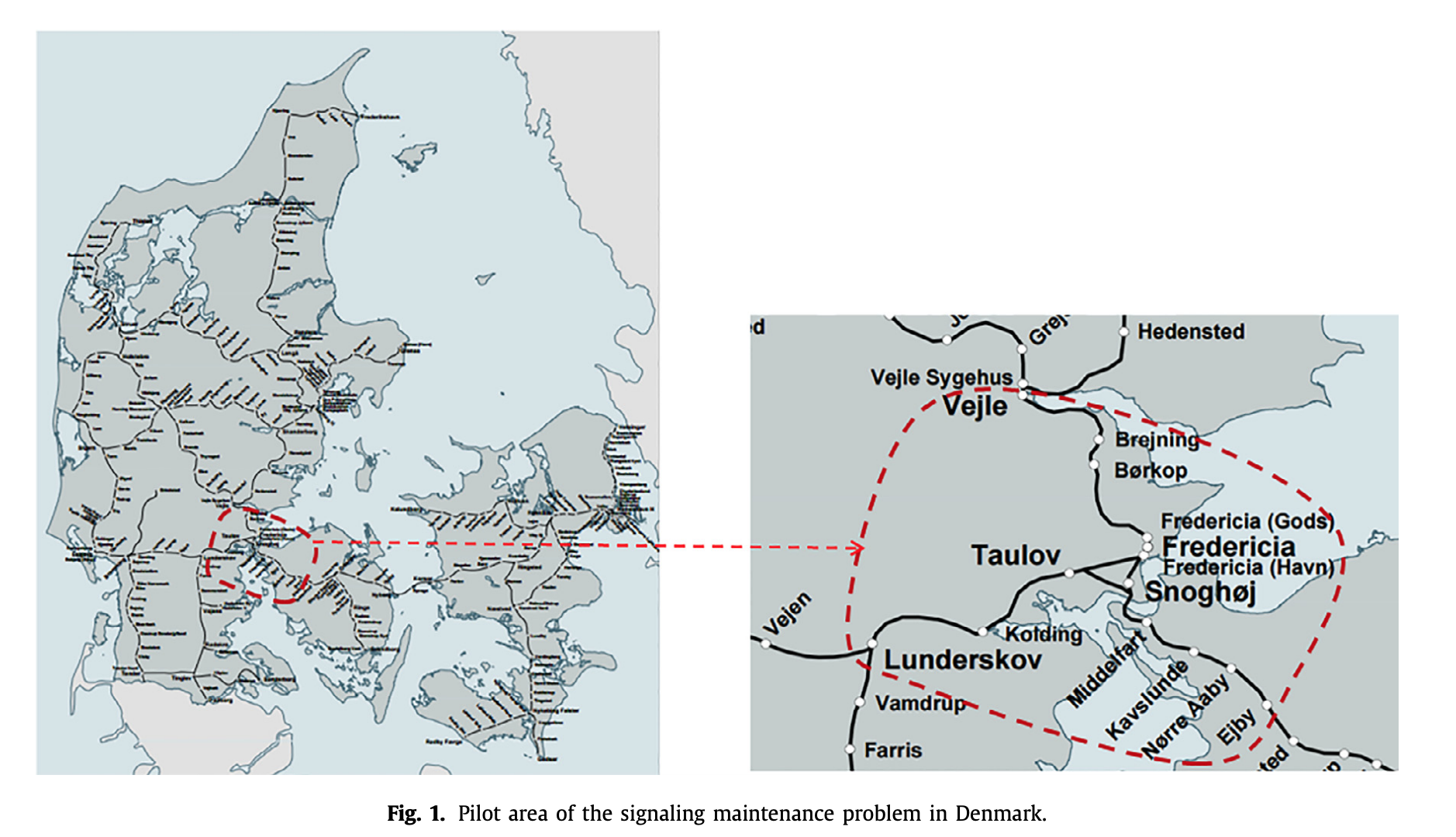
논문에서는 상용 MIP solver를 사용하였으며, 2주의 계획 기간을 고려하여 실험을 진행했다고 한다.
기존 연구
- Cheung, Chow, Hui, and Yong (1999) - 홍콩 대중교통 시스템에 대한 CP 모델 제시
- Gorman and Kanet (2010) - MIP, CP, 유전 알고리즘을 활용한 유지 보수 작업 스케줄링
- Nemani, Bog, Ahuja (2010) - time window, exclusion 제약이 있는 curfew(통행금지) 스케줄링에 대한 4가지 모델 제시
- Bog, Nemani, and Ahuja (2011) - curfew planning에 대해 subproblem의 사이즈를 증가시키면서 반복적으로 푸는 모델
- aper. Peng et al. (2011) - 유지 보수 스케줄링 문제에 대해 클러스터링을 먼저 하고, 경로를 구성해 작업 팀의 이동 비용을 최소화하는 모델
- Borraz-Sánchez and Klabjan (2012) - DP를 이용해 초기해를 만들고, ruin and recreate라는 휴리스틱으로 해를 개선
- Peng and Ouyang (2014) - 여러개의 유지 보수 작업에 대해 preprocessing, constructive phase를 거친 후 local imporvement를 진행.
- Khalouli, Benmansour, and Hanafi (2016) - Ant Colony Algorithm을 사용해 유지 보수 스케줄링 문제 해결
- Baldi, Heinicke, Simroth, and Tadei (2016) - 장기적인 철도 유지 보수 스케줄링 문제에 stochastic한 요소를 도입.
수리 모형
아래 소개할 수리모형은 덴마크의 철도회사 Banedanmark에서 제공받은 것이다.
문제에는 technical places들이 있는데 이는 유지 보수가 필요한 장소를 의미하며, station이나 station 사이에 존재하는 유지 보수 지역이 해당된다.
여기서 crew들은 depot에서부터 작업을 시작해서, 다시 depot로 돌아오며, 이때 crew들의 이동시간, 작업시간 등이 하루 최대 근무 시간을 넘지 않아야 한다.
그리고 각 작업마다 필요한 crew의 능력을 고려해줘야 하며, 한 작업당 최소 인원 수, 최대 인원 수가 정해져 있다.
게다가 하루 이상 걸리는 작업에 대해서는 다음날에도 같은 crew들로 구성해줘야 한다.
모델에서 사용되는 변수와 파라메터에 대한 정의는 다음과 같다.

작업자, 작업, 시간, 능력, 근무지에 대한 집합이 위와 같이 정의되고,
총 근무시간, 작업 시간, 작업별 작업자 수, 작업자별 능력, 근무지간 이동시간 등에 대한 파라메터가 위와 같이 정의된다.


변수로는, 작업자별 작업량, 근무지간 이동 여부 등에 관련된 변수들이 존재한다.
이 문제에서 목적함수는 기본적으로 세개의 부분으로 나뉜다.
첫번째는 작업 일수를 최소화 하는 것이다.
두번째는 한정된 시간 안에 최대한 많은 작업을 소화하는 것이다.
세번째는 특정 작업에 대해 crew member들이 연속으로 배정되지 않아 생기는 패널티를 최소화하는 것이다.
이러한 multi-objective function을 normalize하기 위해, 논문에서는 각 항에 대해 가중치를 주고, 특정 항에서 가능한 최대값을 나눠주었다.
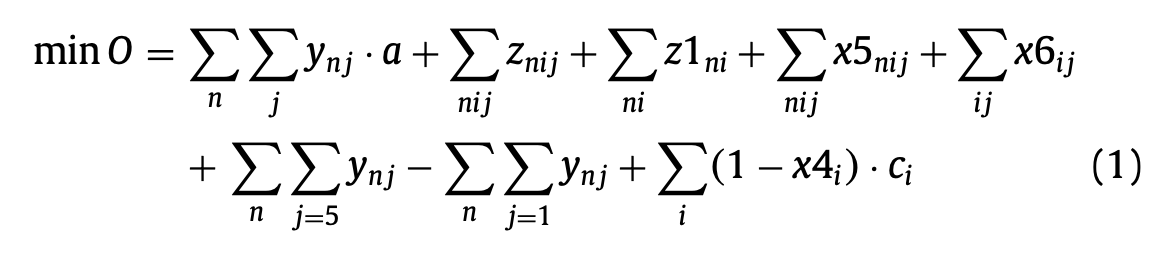
첫번째 항은 작업자들이 일하는 총 시간,
두번째항은 작업자들이 일하는 총 일수,
세번째 항은 작업자들이 일하는 총 작업 수,
네번째 항은 작업자들이 어떤 작업을 연속해서 작업하지 않는 경우의 수,
다섯번째 항은 연속해서 작업되지 않는 작업의 수를 의미한다.
여섯번째 항에서 j는 왜 5인지 잘 모르겠지만, 일곱번째 항과 함께 time horizon초반에 일을 많이 하도록 하는 것 같다.
여덟번째 항은 시간 내에 완료하지 못한 작업들의 시간의 총합을 의미한다.
제약식은 크게 작업과 관련된 제약, 운영과 관련된 제약, 작업자와 관련된 제약, 작업자의 능력, 작업자의 이동과 관련된 제약이 있다.
먼저, 작업과 관련된 제약은 아래와 같은 것들 있다.

(2)는 모든 작업들이 주어진 시간 안에 완전히 끝나거나, 하나도 작업되지 않아야 하도록 한다.
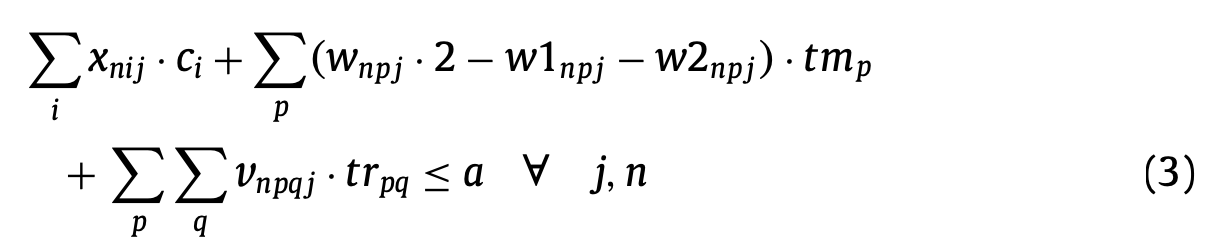
(3)은 각 근무시간이 정해진 시간을 넘지 못하도록 한다.
첫번째 항은 작업 시간이며, 두번째항은 depot에서의 이동시간, 세번째 항은 근무지(technical place)간의 이동시간을 의미하며 우변은 근무당 정해진 시간이다.

(4)는 작업자들의 작업량이 필요로 하는 총 작업량을 넘지 못하도록 한다.

(5)는 하루동안 작업의 일부분만 하는 경우, 작업자들에게 할당된 작업의 총합이 그것과 같도록 한다.

(6)은 주어진 시간 내에 꼭 해야하는 작업에 대해서는 필수적으로 작업을 하도록 한다.

(7)은 작업이 시간 내에 끝나지 못하고 부분적으로 남는 작업이라면, 애초에 못하도록 하는 제약식이다.
즉, 작업을 모두 끝낼 수 있을 때만 부분적인 작업 완성을 허용하는 것이다.

(8)은 작업자가 일하는 날에만 작업을 배정받을 수 있도록 한다.

(9), (10)은 작업자가 어떤 날 작업의 일부분을 할당받았을 때 작업자가 일을 할지 말지에 대한 변수 \(z_{nij}\)값을 1로 만들고, 그렇지 않다면 0으로 한다.

(11)은 작업자가 어떤 날에 작업을 할당받았다면, 어떤 날에 작업자가 일을 할지 말지에 대한 변수인 \(z1_{ni}\)값을 1로 한다.
다음으로, 운영과 관련된 제약으로는 작업이 하루 이상 걸리는 경우에 생기는 제약을 다룬다.
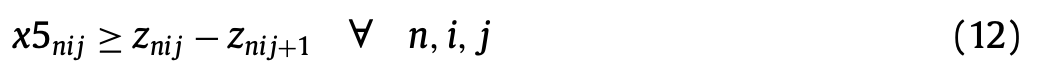
만약 작업자가 \(j\)날에 작업을 했지만 다음 날 작업할 수 없는 경우, 나머지 작업량에 대해서는 남아있는 작업자들이 해야한다.
(12)는 이러한 상황에 대해 패널티를 주기 위한 변수인 \(x5_{nij}\)를 정의한다.

(13)은 작업이 한번에 연속해서 끝나지 않는 경우 패널티를 주기 위한 변수 \(x6_{ij}\)를 정의하는 제약이다.
다음으로, 작업과와 관련된 제약이다.
기본적으로 작업에는 여러 명의 작업자를 투입시키는데, 여기서 인원이 너무 많거나 적을 시 문제가 발생할 수 있다.
따라서 그와 관련된 제약을 다음 (14), (15)와 같이 둔다.


여기서 (14)는 최소 투입 작업자 수, (15)는 최대 투입 작업자 수에 대한 제약이다.

(16)은 작업자의 작업량을 총 작업량에서 최소한의 작업자 수를 나눈 값보다 작거나 같게 해줘서 각 작업에 최소한의 작업자들이 할당될 수 있도록 한다.

(17)은 작업자가 작업할 수 있는 날에만 작업을 하도록 한다.
다음은 작업자의 능력과 관련된 제약이다.
논문의 모델은 각 작업에 대한 작업자의 능력을 고려하며, 이 부분이 가장 복잡한 부분이다.
각 작업에 대해서 작업자의 능력을 고려하기 위해서는 다음과 같은 세가지 시나리오가 존재한다.
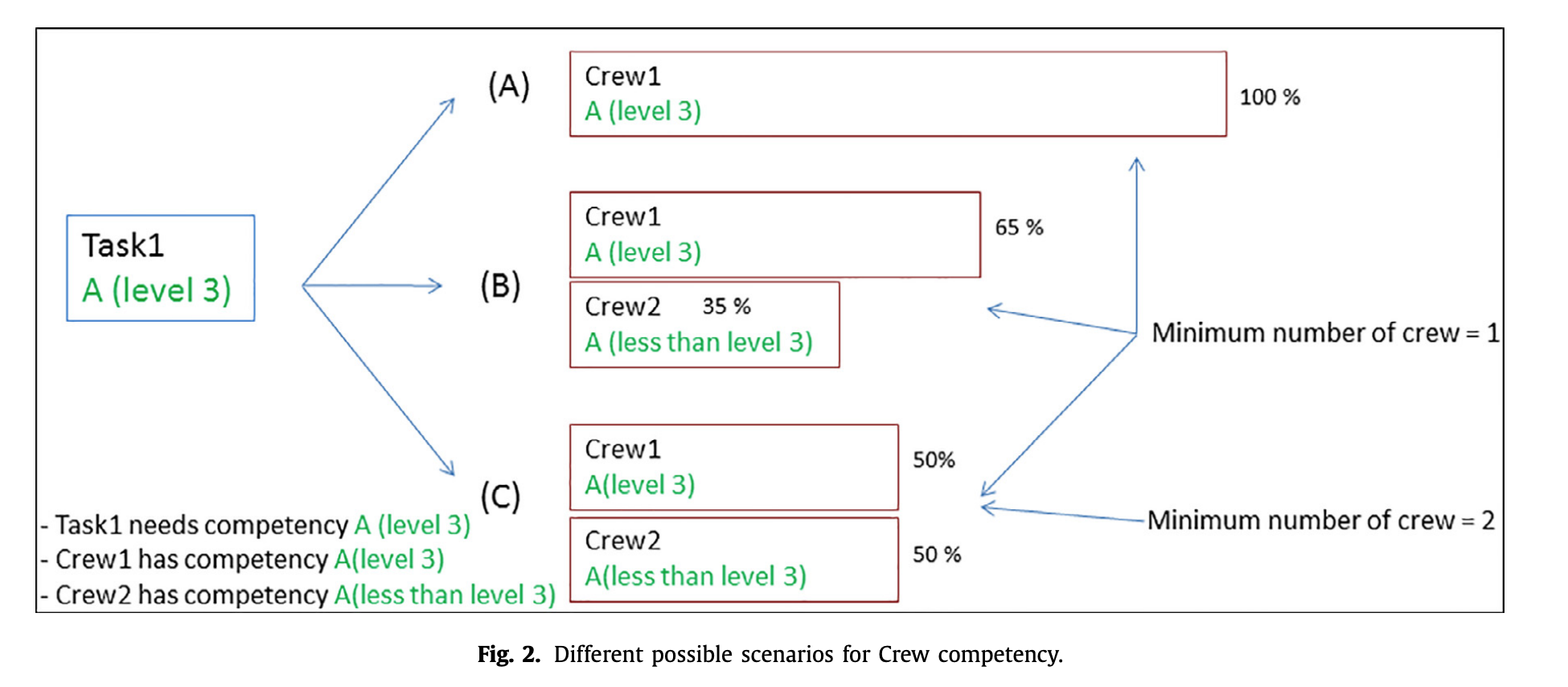
작업은 A라는 능력을 요구하고, 1번 작업자는 3의 숙련도, 2번 작업자는 3보다 작은 숙련도를 가지고 있다고 하자.
이때 작업을 하는 데 한명밖에 필요하지 않다면, 두가지 가능성이 생긴다.
a. 1번 작업자를 투입시키고 모든 작업을 혼자서 하는 방법
b. 2명이 투입하고 능력에 맞게 작업을 할당받는 방법
하지만 이 경우, 작업을 하는데 두명 이상이 필요하다면 다음 방법만이 존재한다.
c. 2명이 작업에 투입되고, 같은 양의 작업을 수행하는 방법
즉, 적어도 한명은 적합한 숙련도(level)를 가지고 있어야 하고, 최소한의 작업자들이 작업에 배정되어야 한다.
이때, 작업자들의 숙련도의 합이 적어도 어느 수준 \(f\)를 넘어야 한다.
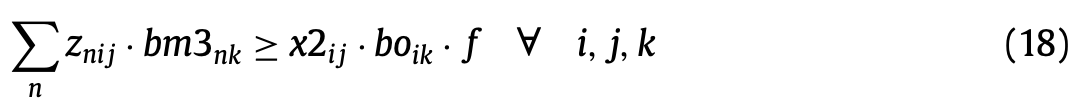
(18)은 작업자들의 숙련도의 합이 어느 수준을 넘도록 한다.
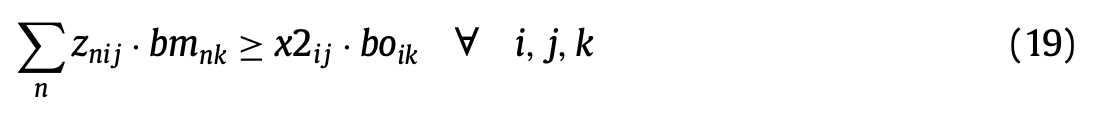
(19)는 적어도 한명의 작업자는 숙련도가 3이 넘어야 한다는 제약이다.
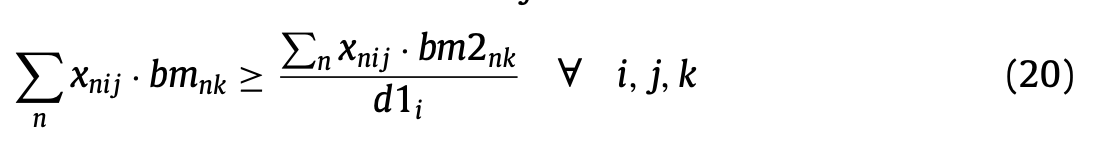
(20)은 여러 작업자들 사이에서 적어도 한명은 3이 넘는 숙련도를 가지도록 하는 제약이다.
마지막으로, 작업자의 이동과 관련된 제약들이 있다.
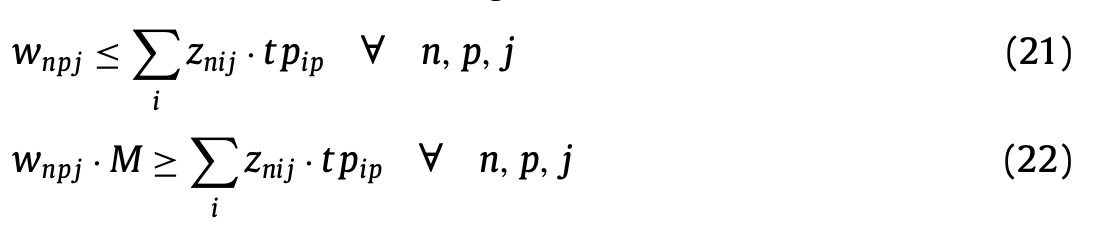
(21), (22)는 작업자의 근무지(technical place)간 이동과 depot에서의 이동과 복귀에 대한 변수인 \(w_{npj}\)를 정의한다.
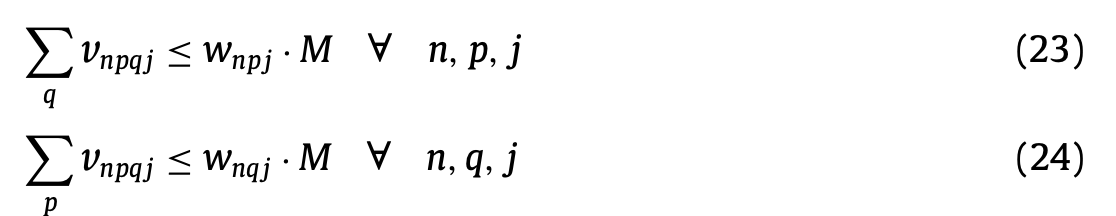
(23), (24)는 작업자가 작업을 배정받은 근무지로만 이동하도록 제약한다.
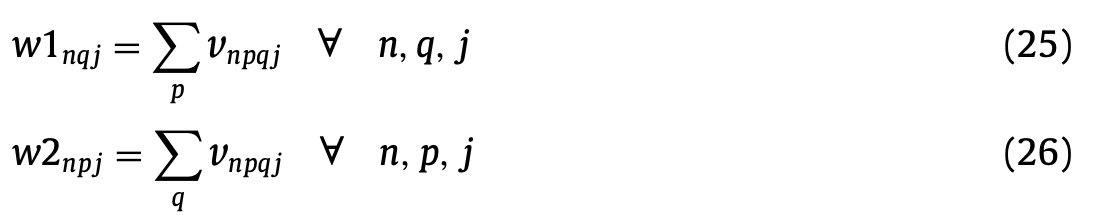
(25), (26)은 작업자가 근무 동안 한개 이상의 근무지를 방문할 경우 어디서 출발했고, 어디로 도착했는 지에 대한 변수를 정의한다.

(27), (28)은 각 작업자는 하루에 한 근무지에 대해서 왔다, 갔다를 한번씩만 할 수 있도록 한다.
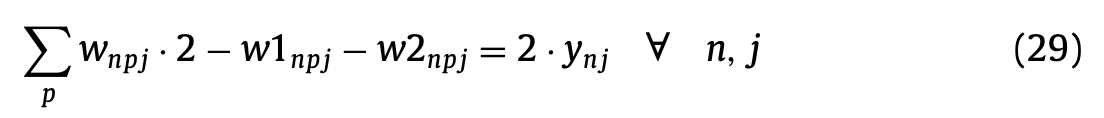
(29)는 작업자가 작업하는 날이라면, depot에서 한번 출발하고, 한번 도착하도록 한다.
논문에서 제안하는 방법
이 논문에서는 사이즈가 큰 문제에 대해서 feasible solution을 찾는 것이 목표이다.
이에, 앞서 말했듯이 CP를 통해 초기해를 만들고, MIP를 통해 해를 개선하는 방법의 two-phase 방식의 기법을 제안한다.
여기서 CP에는 Google OR-Tools를 활용했다.
Construction phase
논문에서는 CP를 만들 때, 문제를 CSP 형태로 만들었다고 한다.
CSP는 변수 집합, 각 변수에 대한 domain 집합, 변수들에 대한 제약 집합의 세가지 집합들의 요소로 수리 모형을 작성만드는 것이다.
각 solution은 한정된 domain내에서 변수에 값을 부여했을 때 모든 제약을 만족했을 때 만들어진다.
논문에서는 작업자들의 능력(competency)에 관한 제약은 global constraint로 하여 모델링을 해줬다고 한다.
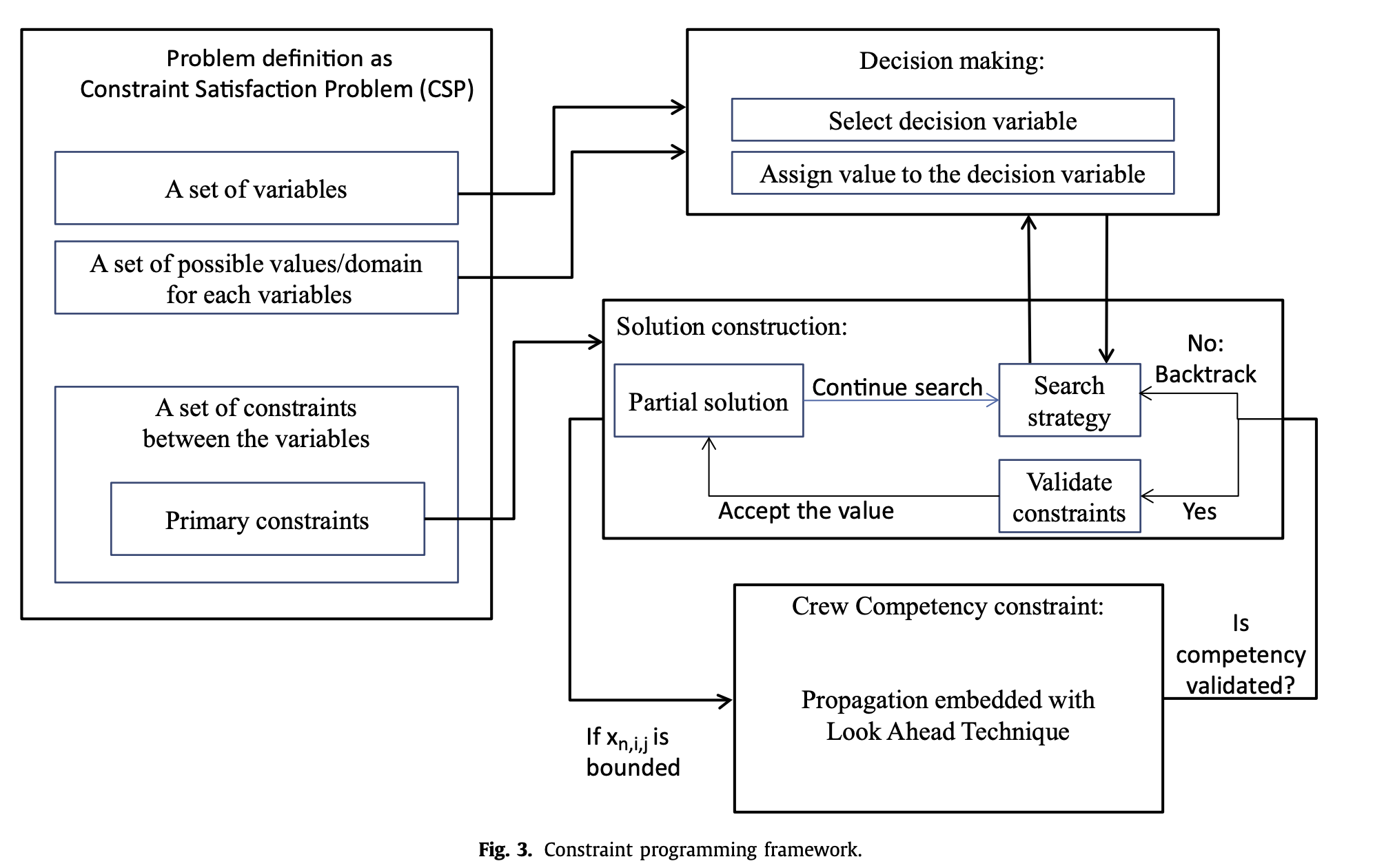
위 그림은 CP의 단계를 설명하는데, CP에는 총 4단계가 있다.
- problem definition
- decision making
- solution construction
- defining the crew competency global constraint
problem definition에서는 문제를 CSP로 만들기 위해서 모든 MIP변수들에 대해 유사한 domain을 적용하여 정의했다.
그리고 작업자의 능력과 관련된 제약을 제외한 모든 제약을 primary constraint로 정의했다. 작업자의 능력과 관련된 제약은 global constraints로 final stage에서 따로 정의한다.
여기서 global constraint란, “expressive and concise condition involving a non-fixed number of variables”이며, 많은 CP모델에서 사용되는 대표적인 global constraint들이 존재한다.
이 논문에서는 문제에 맞는 global constraint를 정의하여 사용했다고 한다.
다음으로, decision making단계에서는 main decision variable을 정의하고 search tree가 만들어지는 방식을 정의했다.
이 문제에서 핵심이 되는 decision variable은 작업자가 언제 어떤 작업을 얼마나 하는지에 대한 변수인 \(x_{nij}\)이다.
tree의 각 노드에서 이 중 한 변수가 선택되고 값이 부여되면서, 탐색 공간 내에서 다른 변수들에 대한 값 역시 값이 부여된다.
Google OR-tools에는 변수를 선택하는 16가지 방법과 값을 부여하는 14가지 방법이 있다.
solution construction단계에서는 각 decision tree의 노드에서 하나의 main decision variable을 선택하고 값을 정한다.
이를 tree-based search strategy라고 하는데, root 노드를 포함한 노드들에서 \(x_{nij}\)를 선택하고 값을 부여한다.
이러한 방법은 look-back, look-ahead 방법으로 개선될 수 있다고 한다.
여기서는 crew competency constraint를 global constraint로 하여 infeasible region을 제거하는데, 이때 propagation algorithm에 들어있는 look-ahead 기법이 infeasibe area를 찾는다.
마지막으로 crew competency constraint를 global constraint로 정의하고 constraint propagation으로 문제를 쉽게 만든다.
이는 crew competency 제약을 어기는 infeasible한 탐색 공간을 줄여주는 방식으로 진행된다.
만약 \(x_{nij}\) 변수의 domain이나 bound가 변한다면 다른 모든 변수의 값을 propagate하는 이벤트를 발생시킨다.
전체 진행 중에서 algorithm 1과 algorithm2가 사용되는데, 이 알고리즘들은 현재 솔루션의 혹은 미래의 잠재적인 솔루션이 crew competency constraint를 충족하는 지 알아보는 알고리즘이다.

위 알고리즘 1은 \(x_{nij}\)가 bounded이거나 domain이 바뀔때마다 호출되는데, 현재 솔루션의 상태를 확인하는 데 사용된다.
이 알고리즘은 작업 \(i\)에 대한 제약조건을 확인할 필요가 있는 지, 필요하다면 솔루션의 정보를 파악하는 데 사용된다.

알고리즘 2는 앞서 얻어낸 솔루션에 대한 정보를 토대로 crew competency 제약을 확인하기 위한 것이다.
Improvement phase
앞선 construction phase를 통해 feasible solution을 얻었다면, 거기서부터 MIP solver를 이용해서 branch and bound를 실행한다.
논문에서는 CPLEX를 사용해서 앞선 수리모형을 구현했다고 한다.
실험 결과
실험에 사용된 데이터셋은 덴마크 철도 회사의 실제 데이터를 사용했고, 다음과 같은 조건을 가진 4개의 문제를 통해 실험을 진행했다.
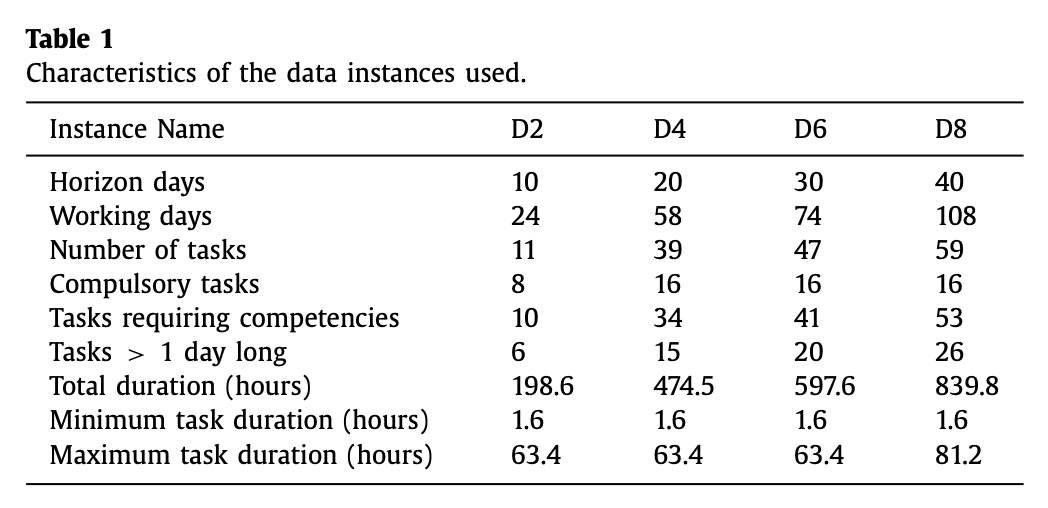
이때 decision making에 Max_Size strategy를 사용하면 feasible solution을 만들지 못했고, Min_Size strategy는 찾는 index의 순서 6가지 중 3가지에 대해서 아래와 같이 feasible solution을 찾았다.
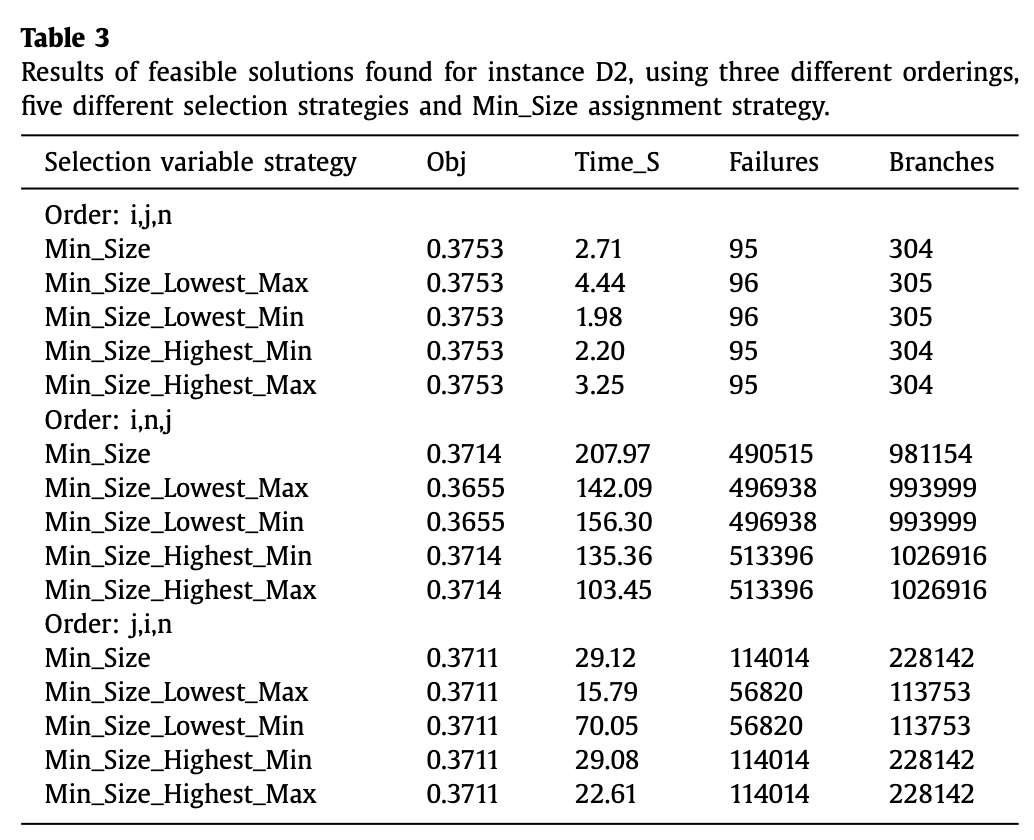
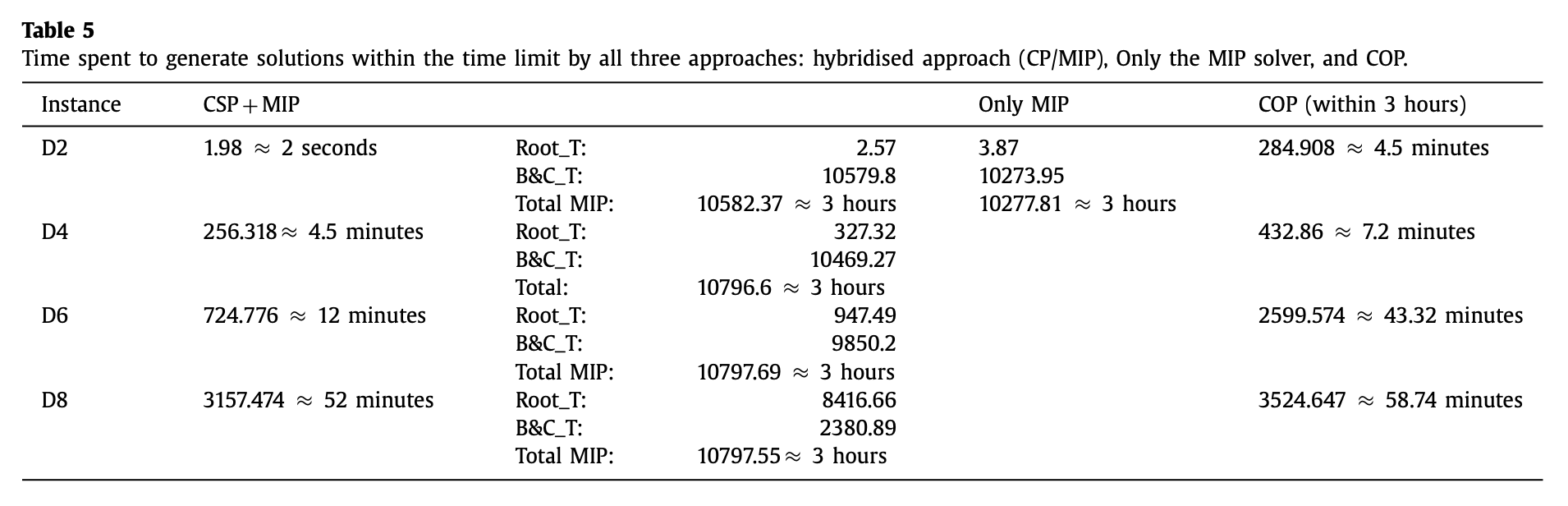
이러한 방식으로 feasible solution을 찾고, 이를 MIP의 warm start를 위해 쓴 hybrid 방식과 순수 MIP, COP와의 결과 비교는 다음과 같다.
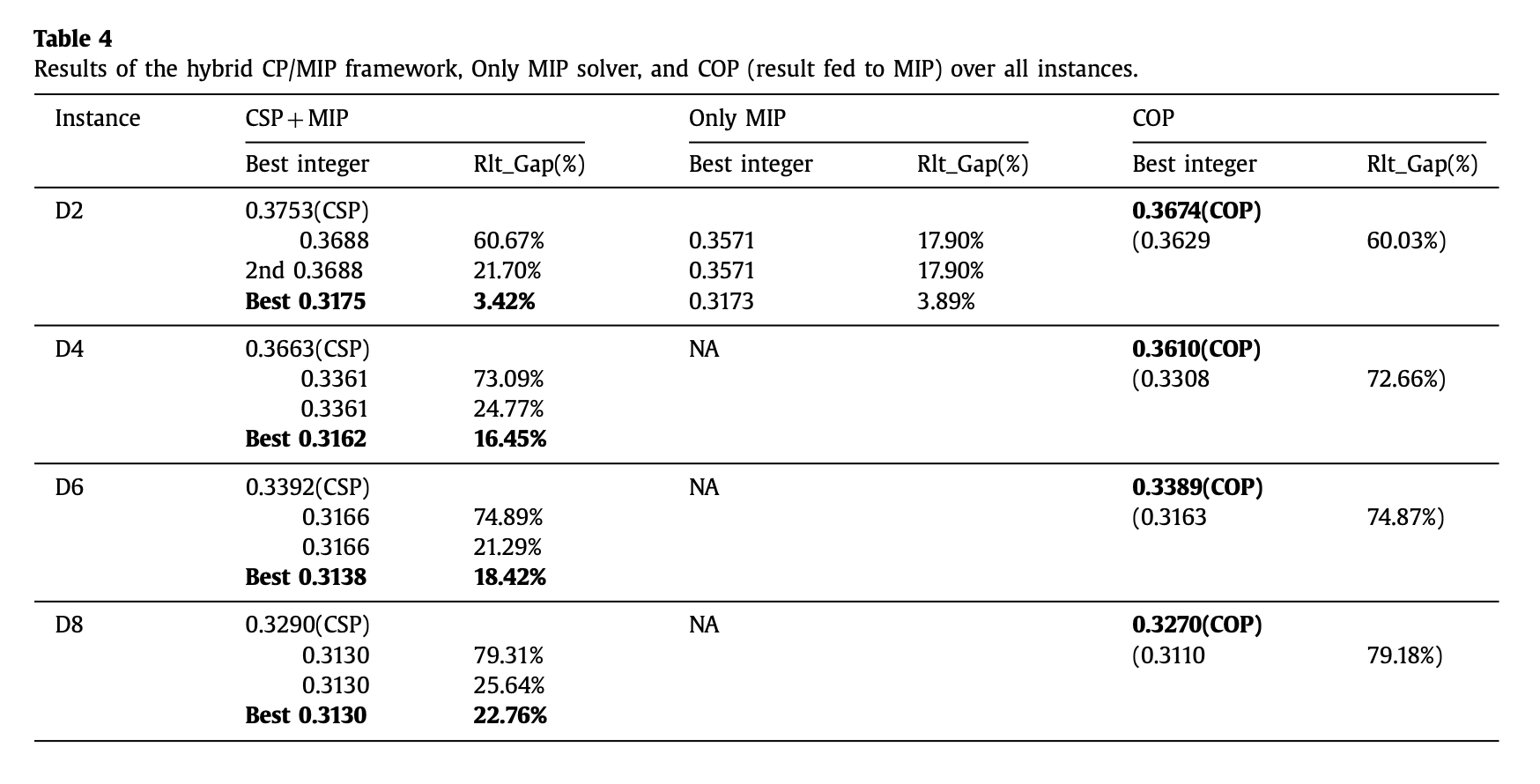
아래는 시간에 대한 비교 결과다.
결론
- 사이즈가 큰 작업자 스케줄링 문제에 대한 hybrid CP/MIP framework 제시.
- CP에 독자적인 global constraint를 사용, look-ahead 기법을 적용하여 초기해를 구함.
- CP를 통해 구한 초기해를 MIP의 warm start에 활용.
- 실험 결과, MIP나 COP를 단독적으로 사용했을 때 보다 시간면에서 훨씬 좋은 성능을 보임.