이번 세미나에서 발표할 논문은 Planning and Scheduling by Logic-Based Benders Decomposition이다.
이 논문은 2007년에 INFORMS지에 발표되었으며 저자는 카네기 멜론 대학의 J. N. Hooker이다.
논문의 주제
논문에서는 생산에서 makespan, tardiness를 최소화하는 planning and scheduling 문제를 다룬다.
이때 mixed-integer linear programming(MILP), constraint programming(CP)를 사용한다.
작업을 설비에 할당하는 문제는 MILP로 풀고, 스케줄링 문제는 CP로 푼 다음, 두 문제를 logic-based Benders decomposition로 연결지어 전체 문제를 해결하는 것이 이 논문의 핵심 아이디어다.
Introduction
생산, 공급망에서 발생하는 스케줄링 문제에서 납기 내에 생산을 완료하도록 작업(Task)들이 설비에 할당이 되어야 한다.
작업들은 자원 제약을 넘지 않는 선에서 병렬적으로 진행될 수도 있으며, 최종적인 목표는 비용, makespan, tardiness를 최소화 하는 것이다.
그런데 이런 문제는 굉장히 어려운 문제이기에, 현실에선 대부분 상식적인 방식으로 문제를 푼다.
중앙 관리자가 작업을 설비에 할당하면, 오퍼레이터가 디테일한 스케줄을 짜는 것이다. 이 과정에서 문제가 있으면 다시 중앙관리자가 작업을 할당하고, 다시 스케줄을 짜는 방식이다.
그런데 이러한 방식은 시간이 굉장히 오래걸리고, 좋은 스케줄이라는 보장도 없다.
이러한 방법에 Benders decomposition 기법을 적용하자면, Master 문제에서 설비를 할당하고, subproblem에서 독립적인 스케줄링 문제를 풀 수 있다. Master 문제에 추가되는 benders cut은 오퍼레이터의 피드백과 같은 것이다. 그리고 모든 할당과 스케줄링이 최적일 때 알고리즘을 끝내는 것이다.
그런데 이 문제에서 전통적인 benders decomposition(BD)은 적합하지 않다.
왜냐하면 전통적인 BD의 subproblem은 continuous한 문제여야 하는데, 스케줄링 문제는 조합 문제이기 때문이다.
하지만 이 논문에서는 BD의 subproblem을 logic-based한 형태로 확장해 스케줄링 문제에 적용하는 방법을 제시한다.
Logic based BD의 다른 장점으로는 MILP와 CP의 장점을 살릴 수 있다는 것이다. MILP는 할당 문제, CP는 스케줄링 문제를 푸는 방식으로, 각자가 잘 풀 수 있는 문제를 풀게 할 수 있다는 것이다. 이 방법으로 상당히 문제를 빠르게 풀 수 있게 된다.
게다가 언제든지 알고리즘을 종료하고, feasible solution을 얻을 수 있다는 장점도 있다.
logic-based BD는 benders cut을 만드는 특정한 기준이 없고, 문제마다 달라질 수 있다.
The Problem
일반적인 생산계획 문제는 다음과 같이 정의할 수 있다.
\(j \in \{1,...,n\}\) : 작업
\(i \in \{1,...,m\}\) : 설비
\(p_{ij}\) : 소요시간
\(c_{ij}\) : 자원소모량
\(r_j\) : release time
\(d_j\) : deadline
\(s_j\) : start time
\(C_i\) : 최대 자원
\(J_{it}\) : \(t\)시간에 \(i\)설비에서 작업하는 작업 \(j\) 집합
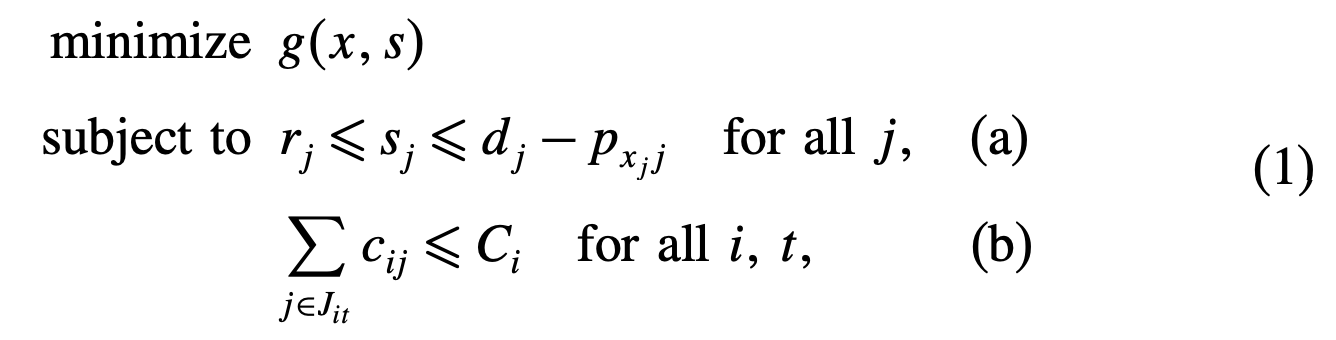
여기에 추가적인 제약을 넣을 수도 있다.
예를 들어, 어떤 작업들은 같은 설비에 할당되어야 한다거나 어떤 작업은 어떤 작업보다 먼저 완료되어야 한다거나 하는 제약을 넣을 수 있다.
그리고 이 논문에서는 다음과 같이 세가지 목적함수를 제안한다.
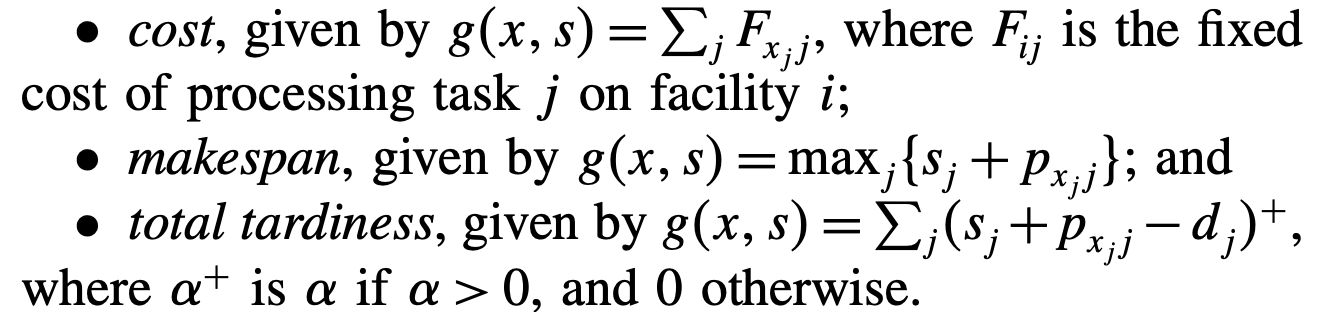
Constraint Programming Formulation
위와 같은 문제를 CP로도 만들 수 있는데, 여기서는 global constraints인 \(element\)와 \(cumulative\)가 사용된다.
\(element(y, v , u)\) : \(v\)는 벡터, \(u\)값을 \(v\)의 \(y\)번째와 동일하게 한다.
\(cumulative(s,p,c,C)\) :
여기서 \(element\)는 equality제약, \(cumulative\)는 inequality 제약?
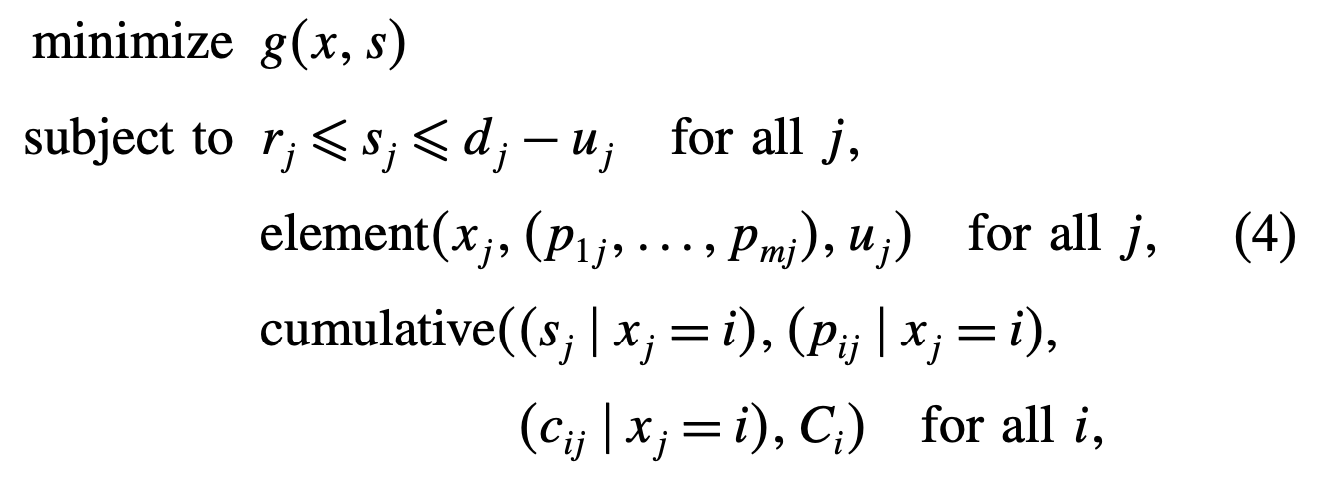
목적식은 cost, makespan 등 원하는 것 선택.
1,2번째 제약식은 시간과 관련된 제약이며 3번째 제약은 자원제약이다.
Mixed-Inter Programming Formulation
이를 MILP로 표현하면 다음과 같다.
\(x_{ijt}\) : \(j\)작업을 \(t\)시간에 \(i\)설비에서 작업한다면 1 아니면 0인 변수
minimum-cost formulation
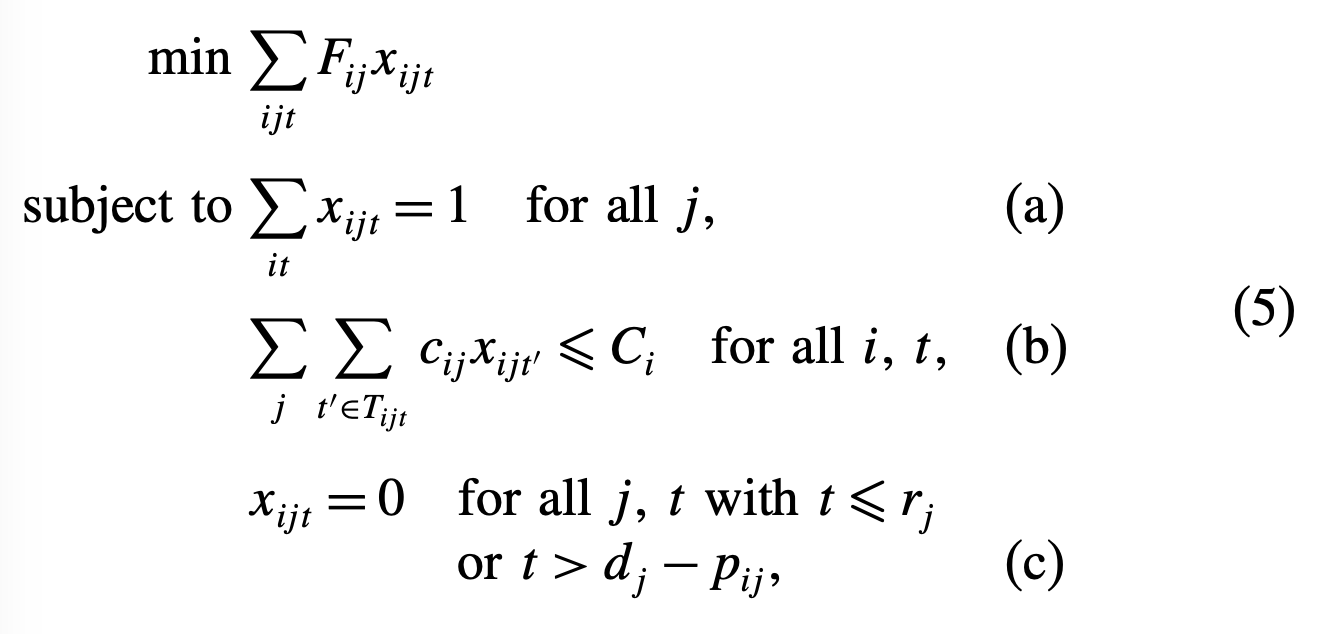
(a) 제약은 각 작업이 한번은 해야한다는 제약이며, (b) 제약은 자원 제약, (c)는 time window 제약이다.
minimum-makespan formulation
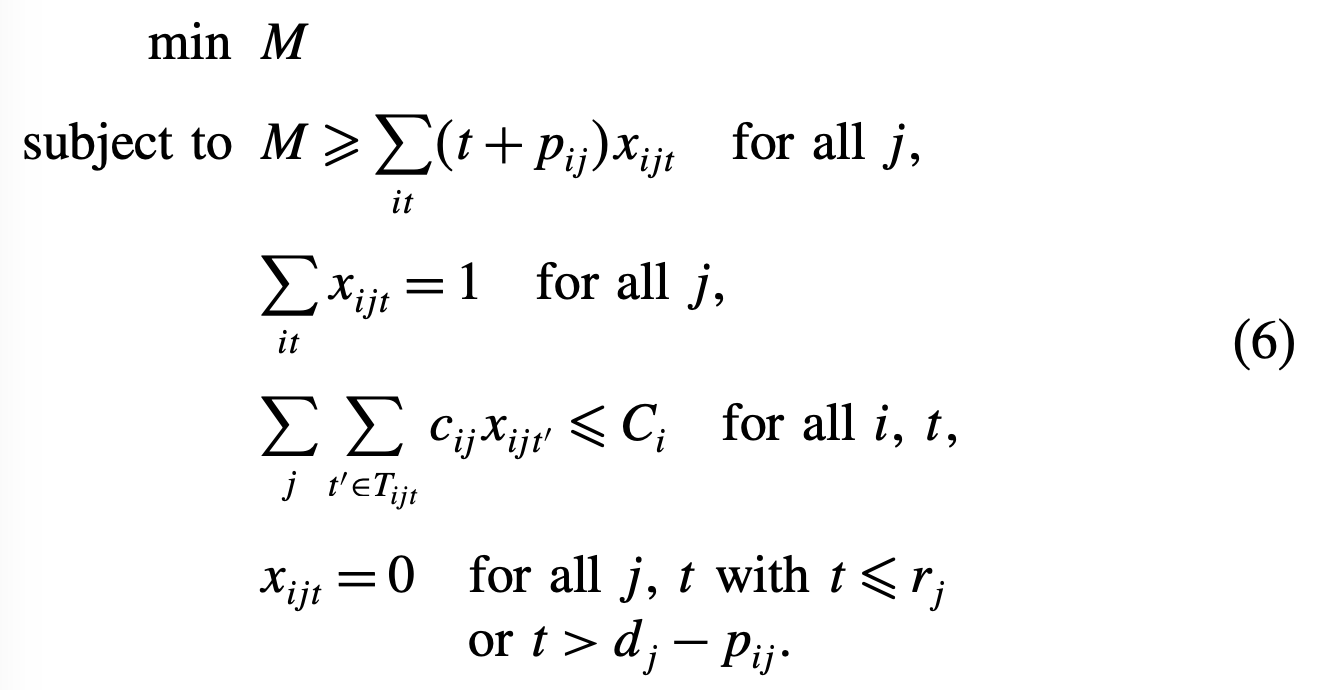
minimum total tardiness formulation
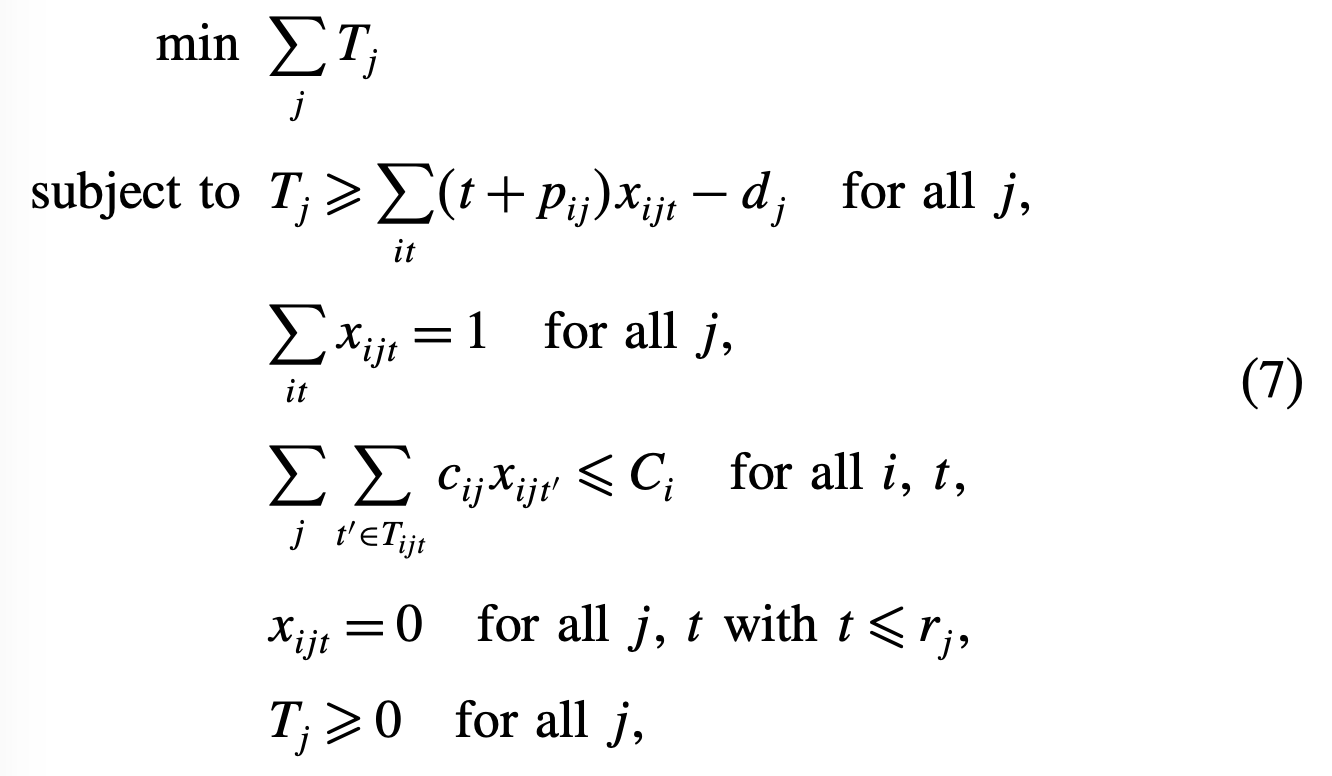
위 포뮬레이션들은 time-indexed한 변수들이기 때문에 확장이 가능하다.
이산적인 이벤트를 가지고 연속된 시간을 사용하는 모델을 살펴보자. \(n\)개의 작업이 있다면 \(2n\)개의 이벤트가 존재하는 것이다.
모델은 각 이벤트에 대해서 각 작업이 끝나는 이벤트인지, 시작하는 이벤트인지 결정한다.
\(x_{ijk}\) : 이벤트 \(k\)는 \(j\)작업이 \(i\)설비에서 시작하면 1아니면 0
\(y_{ijk}\) : 이벤트 \(k\)는 \(j\)작업이 \(i\)설비에서 끝나면 1아니면 0
\(s_{ik}\) : 이벤트 \(k\)가 설비\(i\)에서 시작하는 시간
\(f_{ij}\) : 작업\(j\)가 설비\(i\)에 할당된 경우, 작업\(j\)가 설비\(i\)에서 끝나는 시간
\(R_{ik}\) : 설비\(i\)에서 이벤트\(k\)가 발생할 때 작업들의 자원 총 사용량
\(R^s_{ik}\) : 설비\(i\)에서 이벤트\(k\)가 발생할 때 시작 시 자원
\(R^f_{ik}\) : 설비\(i\)에서 이벤트\(k\)가 발생할 때 종료 시 자원
시작시간과 종료시간에 대한 변수를 나눴기 때문에 자원제약을 만들 수 있다.
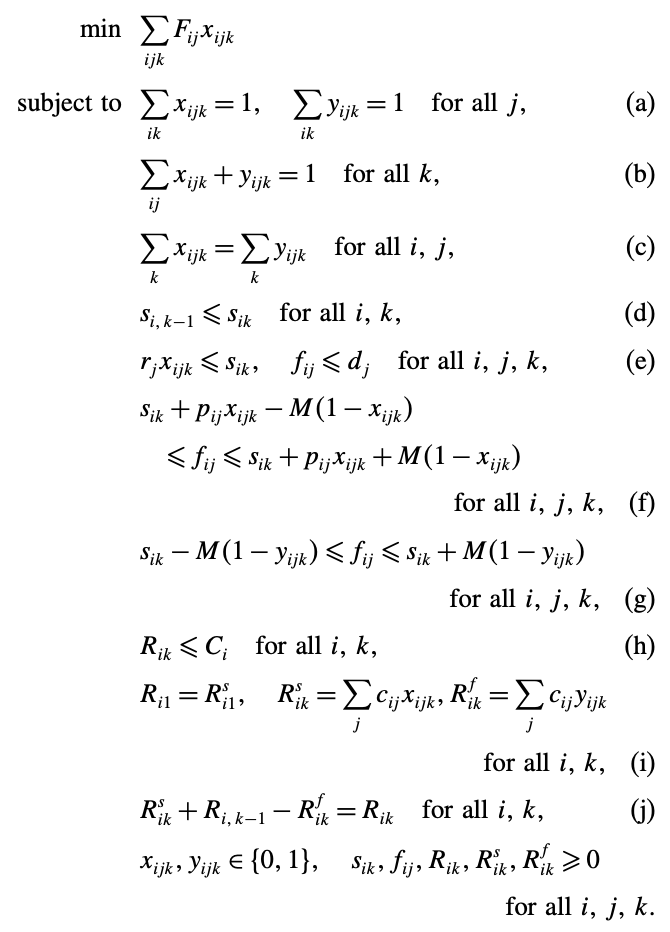
(a)~(c)제약은 각 작업이 설비에 할당되고, 시작과 종료가 한번씩 이뤄져야 하는 것을 의미한다.
(d)제약은 이벤트 1~2n이 순서대로 발생하도록 한다.
(e)제약은 time window 제약이다.
(f),(g)제약은 종료 시간에 대한 변수를 정의한다.
(h)~(j)제약은 자원제약이다.
다음과 같이 포뮬레이션을 만들어주면, 문제는 훨씬 더 어려워진다.
Logic-Based Benders Decomposition
먼저, Benders Decomposition의 큰 틀은 다음과 같다.

그리고 Logic-Based Benders Decomposition은 다음과 같다.
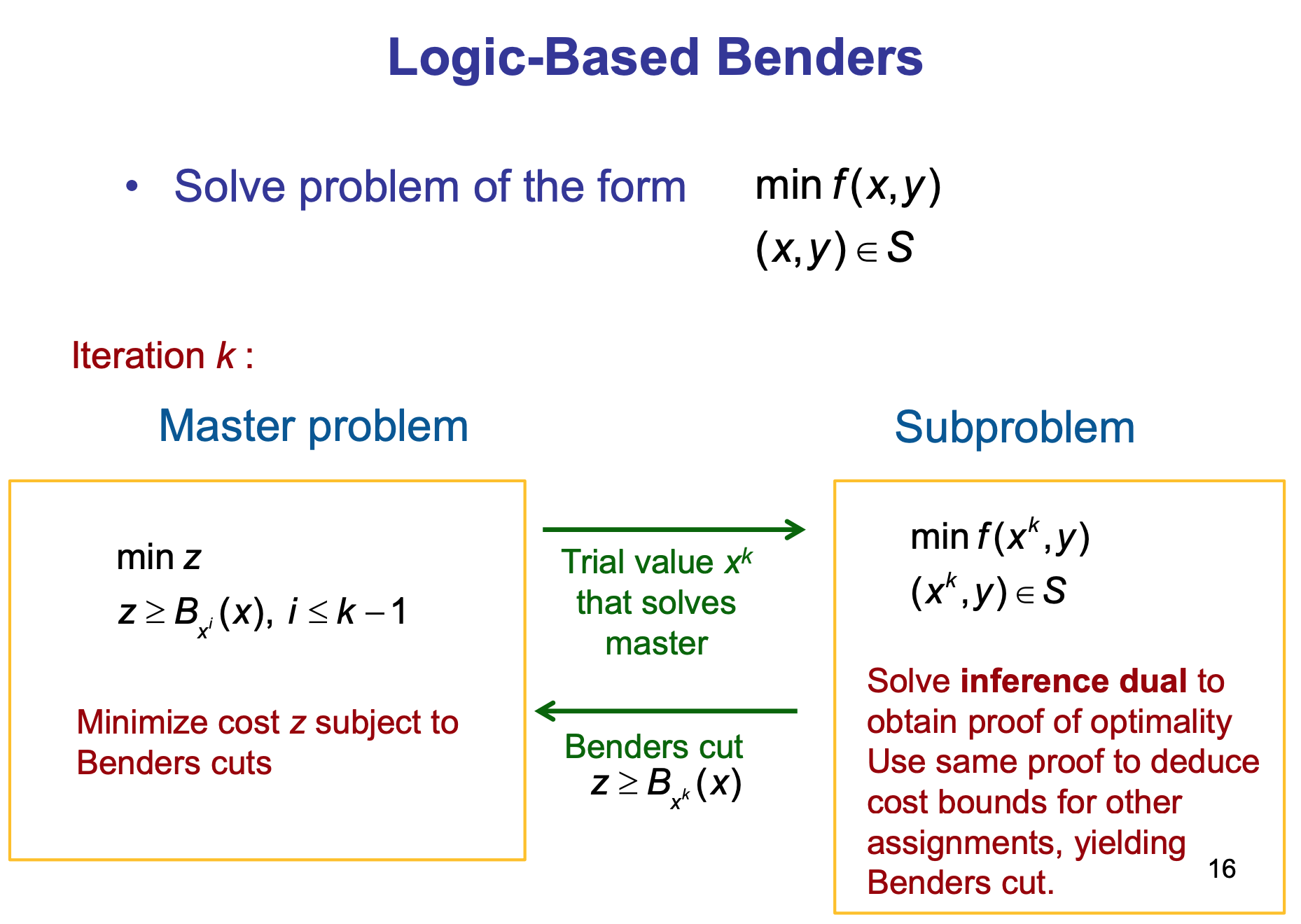
이 과정을 식을 통해 알아보자.
\(C(x,y)\)가 변수 \(x, y\)를 가지는 제약이고, \(D_x, D_y\)가 \(x, y\)의 정의역(domain)이라고 할 때 다음과 같은 formulation에 Logic-based BD를 적용할 수 있다.
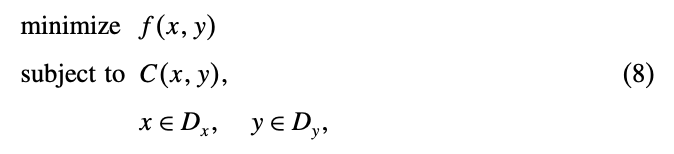
여기서 \(x\)를 \(\bar{x}\)로 고정시키면 다음과 같은 subproblem을 얻을 수 있다.

(9)번의 inference dual은 제약 \(C(\bar{x}, y)\)을 만족하는 \(f(\bar{x}, y)\)에 대한 가장 타이트한 lower bound를 추정하는(infer) 문제다.
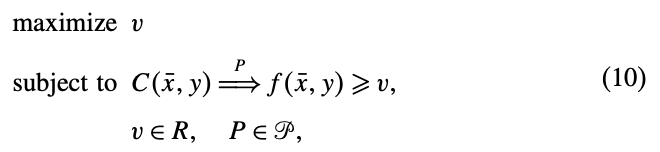
여기서 \(A \Longrightarrow^P B\)의 의미는 “proof P deduces B from A”이다.
이해가 잘 안돼서 다른 자료를 찾아봤는데, “P implies B with respect to A”라고도 한다.
결국 proof P에 대해 A가 만족한다면, B에 대해서도 만족한다는 것으로 이해했다. 식 (10)은 x를 고정시킨 상태의 제약하에, 가장 타이트한 lower bound를 찾는 문제
그리고 \(\mathscr{P}\)는 proof들의 집합이다.
만약 (9)가 LP 문제라면 그 inference dual 역시 LP 듀얼이 되고, \(\mathscr{P}\)에 속하는 proof들은 제약들에 있는 nonnegative linear combinations에 해당한다.
이 듀얼의 솔루션은 \(x = \bar{x}\)일 때 원 문제의 목적함수 \(f(x,y)\)에 대한 가장 타이트한 bound라는 proof라고 볼 수 있다.
기본적으로 Benders Decomposition은 이러한 proof schema를 사용해서 bound \(B_\bar{x}(x)\)를 만든다.
classical BD에서는 여기서 linear combination이 사용된 것이다.
일반적으로 bounding function \(B_\bar{x}(x)\)는 두개의 특성(property)을 가져야 한다.
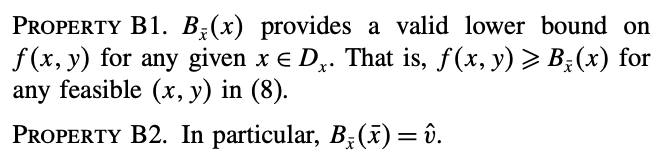
\(B1\) : bounding function은 어떤 feasible \((x,y)\)에 대한 lower bound를 줘야한다.
\(B2\) : fix한 \(x\)를 그대로 넣었을 때 가장 타이트한 바운드다.
여기서, 원 문제(8)의 목적함수값이 \(z\)라고 한다면, \(z \geq B_\bar{x}(x)\)가 Benders cut이다.
그러한 benders cut들을 넣은 master problem을 여러번 반복해서 푸는데, 다음과 같은 식으로 표현될 수 있다.
여기서 \(H\)는 반복횟수다.
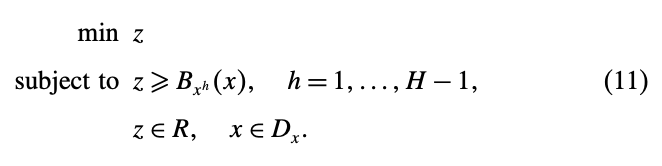
여기서 \(x^1,...,x^{H-1}\)은 이전의 \(H-1\)번의 마스터 문제를 통해 나온 해다.
그리고 master problem의 solution \(\bar{x}\)으로 다음 subproblem을 만든다.
그렇다면 알고리즘은 언제 끝나는가?
이전 \(H-1\)번의 서브문제에서 나온 optimal value들인 \(v^*_1, ..., v^*_{H-1}\)중 최소값인 \(v^*\)와 master problem의 optimal value인 \(z^*_H\)가 같아질 때 끝난다.
\(z^*_H\)는 최적해의 lower bound, \(v^*\)는 최적해의 upper bound이기 때문이다.
 이를 통해, 원 문제나 subproblem이 infeasible이라면 무한대의 optimal value를 갖는다고 받아들일 수 있다.
이를 통해, 원 문제나 subproblem이 infeasible이라면 무한대의 optimal value를 갖는다고 받아들일 수 있다.
다시 (1)번의 생산 스케줄링 문제로 돌아오면, 변수 \(x,s\)는 각각 (8)번의 \(x,y\)에 부합하고 어떤 작업 \(\bar{x}\)를 설비에 할당하면 다음과 같은 서브문제가 만들어진다.
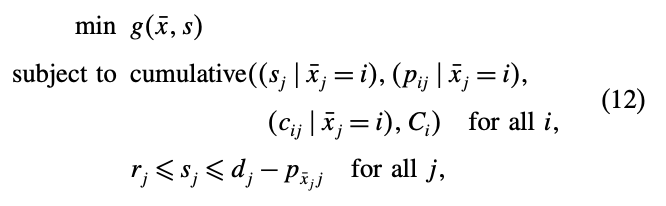
즉, master problem에서 각 작업들을 설비에 할당시킨 것이고, subproblem은 각 설비 \(i\)에 대한 스케줄링 문제가 된 것이다.
이 subproblem을 CP solver로 풀어 Benders cut을 만들 수 있고, 만들어진 benders cut은 master문제의 제약이 되는 것이다.
이때, bounding function \(B_\bar{x}(x)\)는 \(x=\bar{x}\)에 대한 bound의 추론의 유형?(type of reasoning)을 확인하면서 얻어지고, 이 추론은 일반적인 \(x\)를 얻는것으로 확장된다.
Minimizing Cost
cost의 경우 master문제의 변수로만으로도 목적함수 계산이 가능하기 때문에 가장 간단하다.
cost문제에서 subproblem(12)는 feasible할 때 \(\sum_j F_{x,j}\)값을 갖고, infeasible일 때 \(\infty\)를 갖는다.
\(J_{hi} = \{j\|x^h_j=i\}\)를 iteration \(h\)에서 설비 \(i\)에 할당된 작업들에 대한 집합이라고 할 때,
설비 \(i\)에 대해서 feasible한 스케쥴이 없다면 가장 명확한 benders cut은 설비 \(i\)에 대해서 이 집합 \(J_{hi}\)를 할당하는 경우를 제외시키는 것이다.
이 경우, bounding function은 다음과 같은 형태를 갖는다.

\(B_{x^h}\)는 cost function인 \(\sum_j F_{x_jj}\)와 같기 때문에 \(B1\) property를 만족한다.
\(B_{x^h}(x^h)\)가 서브문제의 optimal이기 때문에 \(B2\)역시 만족한다.
이 bound는 굉장히 약한 bound인데, infeasible을 방지하기 위해서 필요하다.
그리고 간단한 greedy 알고리즘을 사용해서 infeasible을 만드는 가능한 작은 집합 \(\bar{J}_{hi}\)을 찾을 수도 있다.
\(\bar{J}_{hi} = J_{hi} = {j_1, ..., j_k}\)로 두고, \(l = 1,...,k\)라 할 때,
설비 \(i\)에 대해서 \(\bar{J}_{hi}\) \ \(\{j_l\}\)에 속하는 작업들을 스케줄링 하고, 만약 feasible한 솔루션이 없다면 \(j_l\)을 \(\bar{J}_{hi}\)에서 제거한다. 그렇다면 \(\bar{J}_{hi}\)가 (13)의 \(J_{hi}\)로 사용될 수 있다.
실험 결과, 이런 식으로 \(k\)번 스케줄링 문제를 다시 푸는 것이 strong한 bound를 찾는 것보다 계산 속도 면에서 훨씬 좋았다.
그래서, 마스터 문제를 보자.
\(h\)번째 iteration에서 infeasible한 스케줄링 문제에 대한 설비 집합을 \(I_h\)라고 하자.
그러면 마스터 문제를 다음과 같이 표현할 수 있다.

여기서 \(x_{ij}\)는 binary 변수이고, (b)는 benders cut들이다.
그리고 master problem에 subproblem의 relaxation을 넣어주는 것이 중요하다.
relaxation은 다음과 같이 얻을 수 있다.
어떤 두 시간 \(t_1, t_2\)가 있을 때, \(t_1\)과 \(t_2\)시간 사이에 작업되는 작업들의 집합을 \(J(t_1, t_2)\)라고 하자.
만약 그러한 작업들이 작업 \(j\)가 같은 설비 \(i\)에 할당된다면, 이 작업들의 자원 소모량(energy)은 \(t_1\)과 \(t_2\)시간 사이에 \(C_i(t_2-t_1)\)을 넘어서는 안된다(자원제약!). 이 점을 이용해서 다음과 같은 valid inequality를 만들 수 있다.
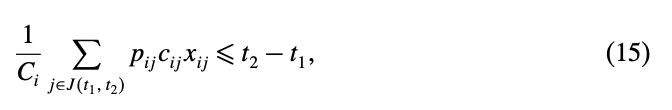
이러한 inequality를 \(R^i(t_1,t_2)\)라 하자.
이때 만약 release time을 오름차순으로 정렬한 \(\{r_1, ..., r_n\}\)을 \(\bar{r_1}, ..., \bar{r_{n_r}}\)이라고 하고, \(\bar{d},...,\bar{d_{n_d}}\)에도 마찬가지로 했을 때, 우리는 각 작업 \(i\)에 대해서 다음과 같은 inequality를 얻을 수 있다.
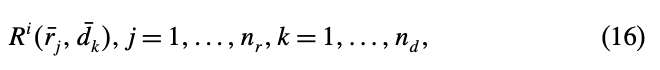
이 제약이 (14)의 (c)에 들어가게 되는 것이다. 각 시간 범위 내에서 자원제약을 넣어주는 것이다.
하지만, \(x_{ij}\)변수를 linear relaxation해야한다.
모든 inequality들이 필요한 것은 아니기 때문에 일부는 생략할 수도 있다.
\(T^i(t_1, t_2)\)를 다음과 같이 정의하자.
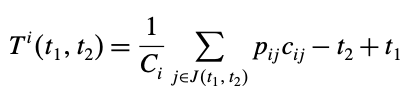
이를 통해, 어떤 \(R^i(t_1, t_2)\)제약이 더 타이트한 지 알 수 있다.
만약 시간 \([t_1,t_2]\)가 \([u_1,u_2]\)안에 포함되고, \(T^i(t_1, t_2) \geq T^i(u_1, u_2)\)라면 \(R^i(t_1, t_2)\)이 \(R^i(u_1, u_2)\)를 dominate하는 것을 알 수 있고, dominated된 \(u_1, u_2\)에 관한 inequality들은 지울 수 있다.
각 설비에 대해 undominated inequality를 찾는 알고리즘은 다음과 같다.

이 알고리즘은 복잡도가 \(O(n^3)\)이다. 하지만 전처리 과정에서 한번만 해주면 된다.
현실적으로, release time(\(r_j\))를 모두 0으로 하여, relaxation을 간소화할 수 있다.
이 방법으로는 불필요한 inequality를 \(O(n)\)의 복잡도로 제거할 수 있고, 알고리즘은 다음과 같다.
반대로, deadline을 마지막 시간으로 고정하는 방법도 가능하다.

Minimizing Makespan
Makespan의 경우에는 subproblem이 최적화문제이기에 조금 더 복잡하다.
하지만 모든 작업이 같은 release date를 갖는다면 간단한 선형 benders cut을 구할 수 있다.
이 문제의 경우, Benders cut은 다음 사실에 기반한다.

즉, 작업들 중 일부를 제외하고 푼 경우, 원래문제의 makespan보다 짧을 수 밖에 없다.
그리고 짧은 정도가 제외된 작업 소요시간의 총합 + 작업 중 가장 늦은 deadline - 가장 짧은 deadline보다 작다는 것이다.
특히, 모든 deadline이 같다면 제외된 작업 소요시간의 총합 보다 작다.
자, 이제 benders 알고리즘의 iteration에서 모든 time window가 같다고 할 때, \(J_{hi}\)를 이전 iteration \(h\)에서 설비 \(i\)에 할당된 작업들의 집합이라고 하자. 그리고 \(M^*_{hi}\)를 그 설비 \(i\)에 의해 발생하는 최소 makespan이라고 하자.
이때 master problem에서 설비 \(i\), 작업 \(j\)에 대해 \(x_{ij} = 0\)라면, 더이상 작업 \(j\)가 \(J_{hi}\)에 속하지 않게 될 것이다.
그렇기에 lemma 2에 의해, 설비 \(i\)에 대한 최소 makespan은 최대 다음과 같다.
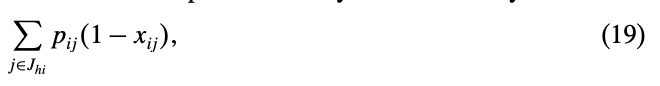
그렇기 때문에, 설비 \(i\)에 대한 makespan의 lower bound는 다음과 같다.

즉, 한 설비에 대한 현재까지의 optimal에서 제외된 작업들의 소요시간의 총합을 뺀 것이 lower bound가 되는 것이다.
이를 통해 다음과 같은 bounding function을 구할 수 있다.
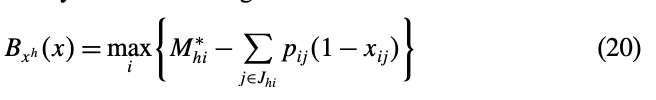
lower bound중 가장 타이트한 bound를 찾는 것이다.
이는 \(B1, B2\)특성을 모두 만족한다.
그리고 이 역시 더 작은 집합 \(\bar{J}_{hi}\)를 통해 강화될 수 있고, greedy 알고리즘으로 찾을 수 있다.
\(\bar{J_{hi}} = {J_{hi}} = \{j_1,...,j_k\}\), \(l = 1,...,k\)일 때,
어떤 설비 \(i\)에 대해 \(\bar{J_{hi}}\) \ \(\{j_l\}\)에 속한 작업들에 대한 최소 makespan을 찾는다.
그리고 만약 최소 makespan이 \(M^*_{hi}\)이라면 \(\bar{J_{hi}}\)에서 \(j_l\)을 제거한다.
그리고 \(\bar{J_{hi}}\)를 (20)의 \(J_{hi}\)으로 사용한다.
그리고 이 Benders cut을 사용하여 다음과 같은 master problem을 만들 수 있다.
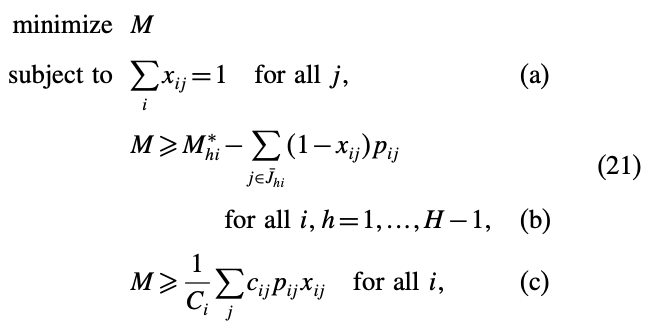
여기서 (c)의 relaxation은 cost문제와 비슷하게 해줄 수 있다.
deadline이 다른 경우, 식 (17)은 만약에 작업이 하나라도 제거되었다면 각 설비 \(i\)의 최소 makespan은 적어도 식 (22)와 같아야 한다는 것을 의미한다.
하지만 작업이 하나라도 제거되지 않았다면, 그대로 \(M^*_{hi}\)인 것이다.
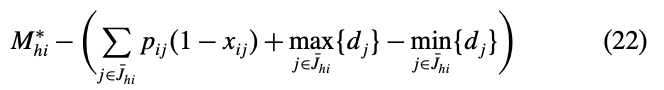
설비 \(i\)에서 \(\bar{J}_{hi}\)에 속한 어떤 작업도 제거되지 않는다면, (23)의 두번째 제약은 \(w_{hi}\)을 0으로 만들고, bound는 \(M^_{hi}\)가 된다. 만약 하나 이상의 작업이 제거되었다면 bound가 (22)가 된다.
그리고 deadline이 다르고 release time이 같은 경우 benders cut (23)이 식 (21)의 benders cut (b)로 사용된다.
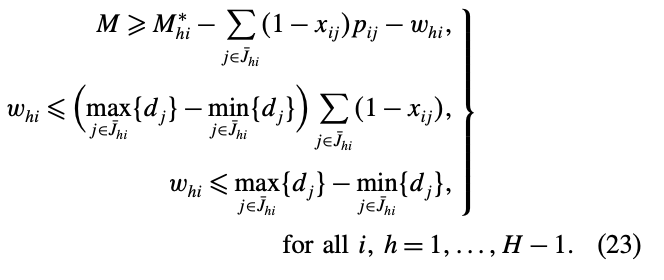
Minimizing Total Tardiness
…
Computational Results
- random generated problem에 대해 실험 - 시간 비교
- MILP(CPLEX), CP(ILOG Scheduler), logic-based BD
-
1~4개의 설비에 대한 cost, makespan 문제 실험 결과
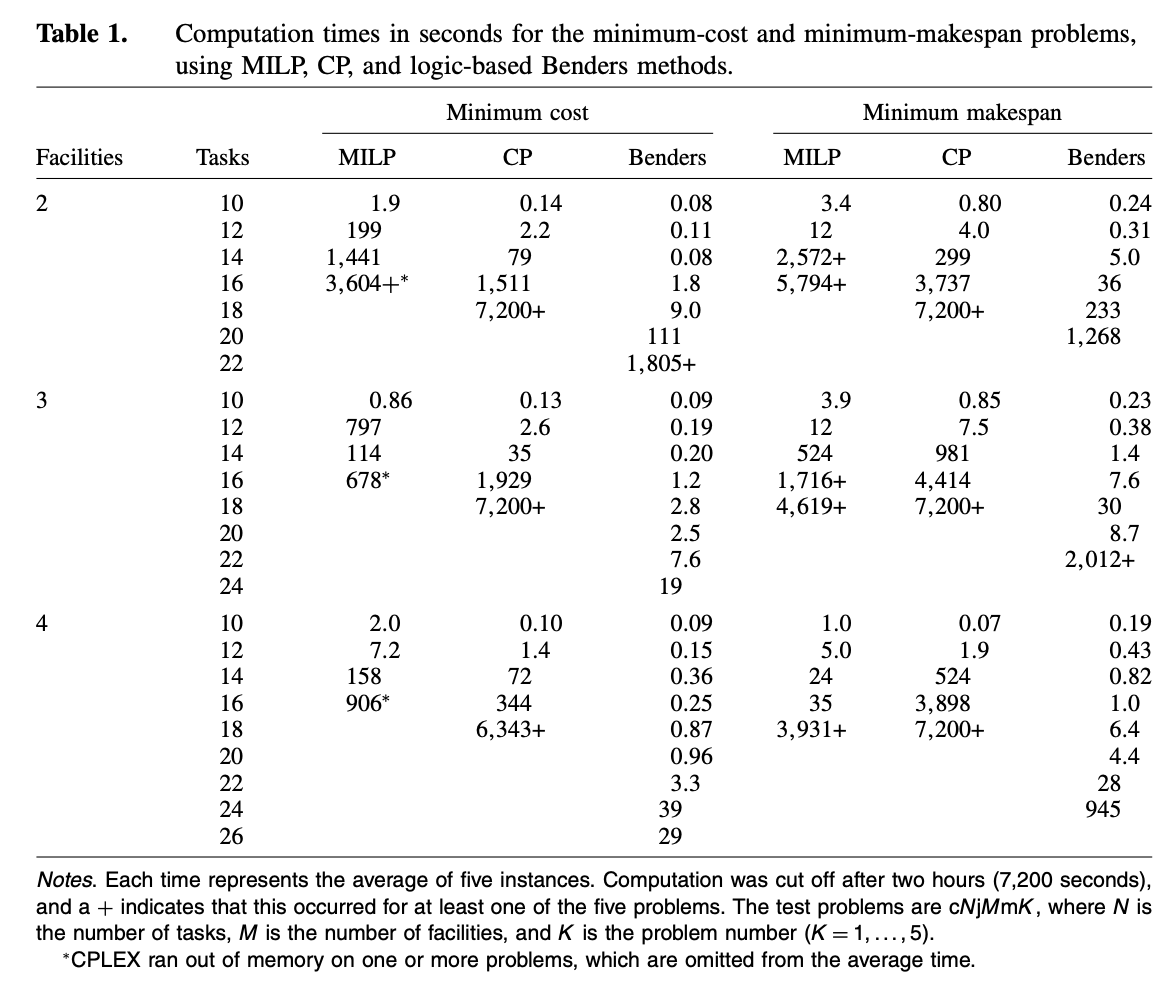
- CP solver가 MILP보다 빠르지만 logic-BD가 그것보다도 빠르다. 심지어 문제 사이즈가 커져도 상당히 빠르게 푼다.
-
다양한 문제에 대한 실험 - 시간 비교
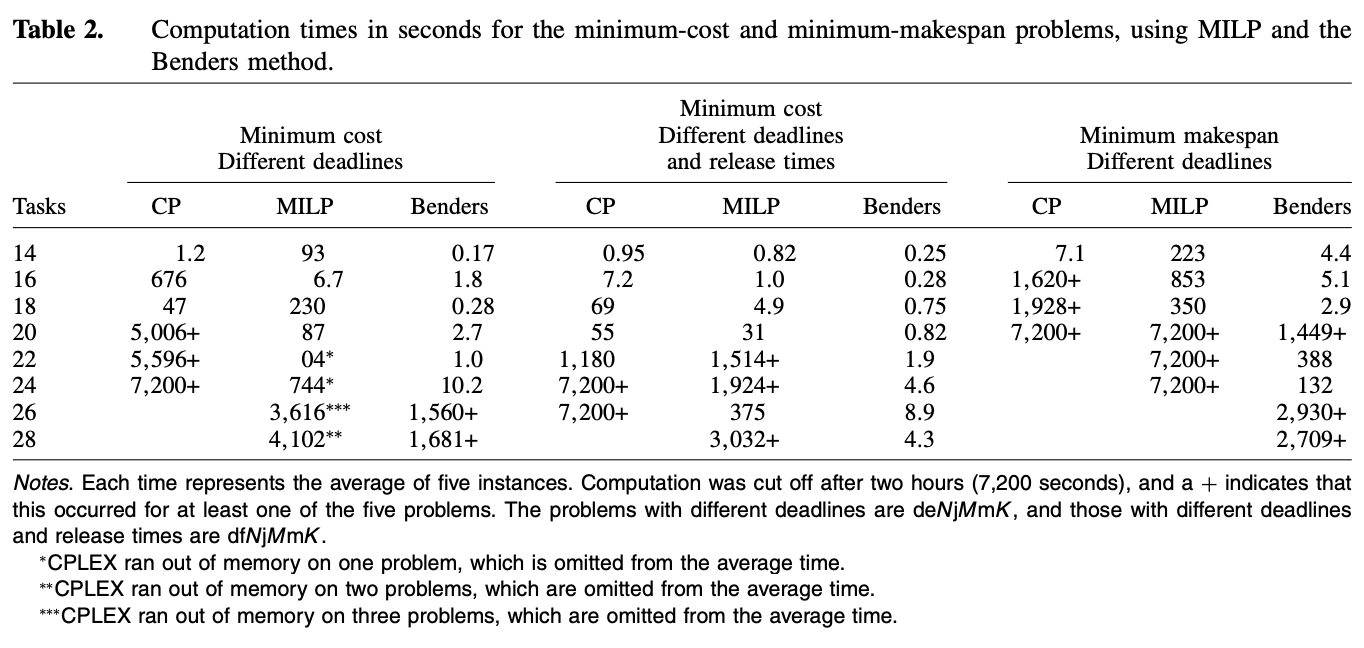
- 역시 logic-BD가 괴장히 빠른 성능을 보인다.
-
Logic Based Benders Decomposition 시간 실험
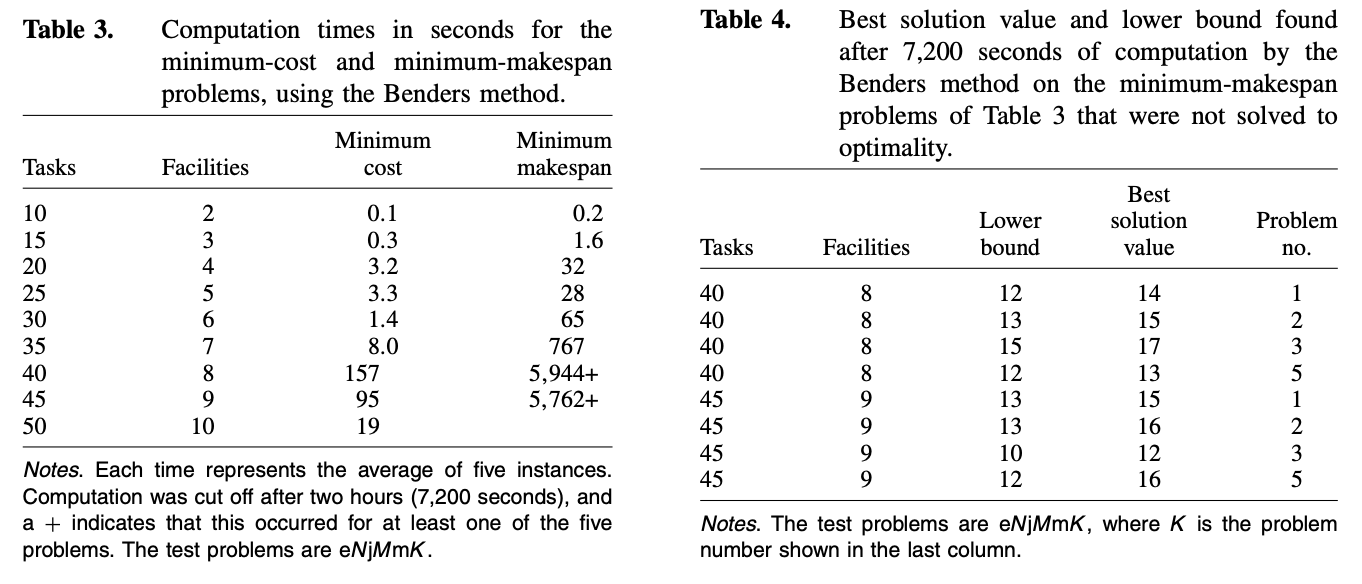
결론
-
스케줄링 문제에 대한 logic-based Benders decomposition 기법 소개
-
CP나 MILP보다 상당히 좋은 성능을 보임
-
상당히 큰 문제에 대해서 최적해를 찾지는 못했지만 feasible solution을 얻을 수 있다.