이번 세미나에서 발표할 논문은 A Green Vehicle Routing Problem이다.
무슨 논문인가?
이 논문에서는 대체연료차량(AFV)의 충전을 고려하는 VRP문제를 푼다.
연구의 목적과 필요성
2009년 미국에서의 총 온실가스 배출량의 28%가 교통분야에서 나왔다. 이에, 화석 연료 사용을 줄이기 위한 많은 노력들이 있어왔다. 그러한 노력 중 하나가 화석연료를 바이오디젤, 전기, 에탄올, 수소, 천연가스 등과 같은 대체 연료로 바꾸는 것이다. 실제로, 정부나 지자체를 비롯하여 여러 기업들이 대체연료차량(AFV)로 운송수단을 바꾸고 있는 상황이다. 이러한 변화가 절실한 이유는 운송에 쓰이는 트럭들은 전체 차량 중에 4%밖에 되지 않지만, 미국의 온실가스배출의 19.2%를 차지하고 있기 때문이다.
이 논문에서는 대체연료를 사용하는 차량들이 충전소를 찾기 어려운 문제가 있고, 많은 기업이나 기관들이 최소한의 비용으로 고객들을 serve하고자 한다는 점에서, 연료가 부족할 위험을 줄임과 동시에 최단경로를 찾고자 한다. 그리고 이러한 문제를 G-VRP(Green Vehicle Routing Problem)이라 이름붙였다.
G-VRP문제에서는 depot, customer, AFSs(대체연료차량충전소)을 의미하는 node들이 있으며, depot을 지나서 customer을 최소한의 거리로 serve하고나서 다시 depot로 돌아오는 것이 목적이다. 이때 차량의 주행거리는 차량 연료의 capacity를 넘지 못하기 때문에 경로 중간에 AFSs를 거쳐 충전을 해야한다.
이 논문에서는 G-VRP를 mixed-integer linear programming(MILP)로 포뮬레이션했다.
문제에 대한 예시
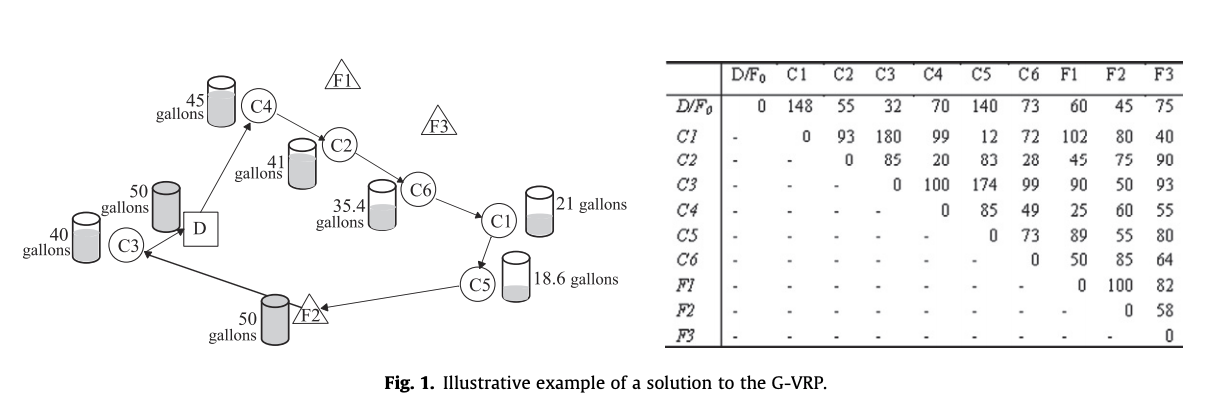
위 예시에서 트럭이 한대있고 차량의 연료 capacity는 50갤런이며, 1마일당 0.2갤런을 소비한다고 하자. 그리고 3개의 AFSs(F1,F2,F3)가 있다. 차량은 depot D에서 출발해서 C1~C6을 거쳐서 다시 D로 돌아와야 한다. 이때 C1~C6을 방문하기 위해서는 339마일을 주행해야하고 이는 67.8갤런을 필요로 한다. 즉, 차량의 capacity보다 17.8갤런이 더 필요한 것이다. 그래서 차량은 최소한 한번은 충전소를 방문해야만 한다. 이때 충전소를 방문한다면 354마일을 주행해야하며, 이는 기존의 최단경로보다 15마일 더 길다.
논문에서 제안하는 방법
VRP문제는 NP-hard문제로 알려져 있고, G-VRP는 VRP의 특별한 경우이므로, G-VRP역시 NP-hard이다. 그렇기 때문에 문제 사이즈가 큰 경우, exact solution을 찾기가 어렵다. 따라서 논문에서는 두가지 휴리스틱 기법 Modified Clarke and Wright Savings(MCWS)와 Density-Based Clustering Algorithm(DBCA)을 사용하여 문제를 푼다.
문제 정의와 G-VRP 수리모형
먼저 문제 설명에 사용되는 기호들의 정의는 다음과 같다.
\(I\) : 고객 노드 집합 \(\{v_1, v_2, ..., v_n\}\)
\(v_0\) : depot 노드 (충전소 역할도 한다.)
\(F\) : 충전소 노드 집합 \(\{v_{n+1}, v_{n+2}, ..., v_{n+s}\}\)
\(V\) : 네트워크의 모든 노드 집합, \(I \cup v_0 \cup F = \{v_0, v_1, ..., v_{n+s}\}\)
\(E\) : 네트워크의 모든 아크 집합, \(\{(v_i, v_j): v_i,v_j \in V, i < j\}\)
\(G(V,E)\) : 노드 \(V\)와 아크 \(E\)로 구성된 그래프
\(t_{ij}\) : 노드 \(i\) 에서 \(j\)로 가는 데 걸리는 시간
\(c_{ij}\) : 노드 \(i\) 에서 \(j\)로 가는 데 걸리는 비용
\(d_{ij}\) : 노드 \(i\) 에서 \(j\)까지의 거리
\(T_{max}\) : 연료 용량으로 인해 생기는 최대 주행가능 시간
논문에서 문제에 대한 가정을 몇가지 하는데, 먼저 모든 아크에 차량의 속도는 같다고 가정한다. 그리고 주행 중에 충전소를 방문하는 횟수에는 제한이 없으며 한번 충전하면 연료는 최대용량만큼 충전된다고 가정한다. 그리고 depot에서 어떤 고객으로 갈 때 적어도 충전소를 한번만 거치면 직접적으로 방문할 수 있다고 가정한다.
G-VRP는 차량이동거리를 최소화하면서 어떤 노드집합을 지나는 각각의 차량에 대해서 최대 \(m\)개의 tour를 찾아야 하며, 각 차량은 depot에서 출발하고 도착한다.
이를 위해 포뮬레이션에서는 고객을 방문하는 것과 AFSs나 depot를 방문하는 것을 구별한다. 왜냐하면 AFSs는 여러번 방문할 가능성이 있기 때문이다. 그리고 depot의 경우에는 출발과 도착점이며 역시 AFS의 역할을 할 수 있기 때문이다. 이렇게 여러번 방문할 수 있는 노드를 위해서 dummy노드 \(s'\)의 집합 \(\pi = \{v_{n+s+1}, v_{n+s+2}, ..., v_{n+s+s'}\}\)을 이용해서 그래프 \(G(V,E)\)를 확장한다. 이와 같은 방법으로 생기는 노드는 \(V' = V \cup \pi\)가 된다. 그리고 각 충전소마다 생기는 dummy node들의 개수는 해당 충전소를 방문할 수 있는 횟수로 정해지며 \(n_f\)라 정의한다. 이 \(n_f\)는 네트워크의 크기를 고려하여 최대한 작은 수로 정의되어야 하지만 효율적인 경로를 위해서라면 충분히 큰 수로 정의되어야 할 필요가 있다.
G-VRP 포뮬레이션에 사용된 기호들에 대한 노테이션은 다음과 같다.

그리고 다음은 G-VRP 포뮬레이션이다.
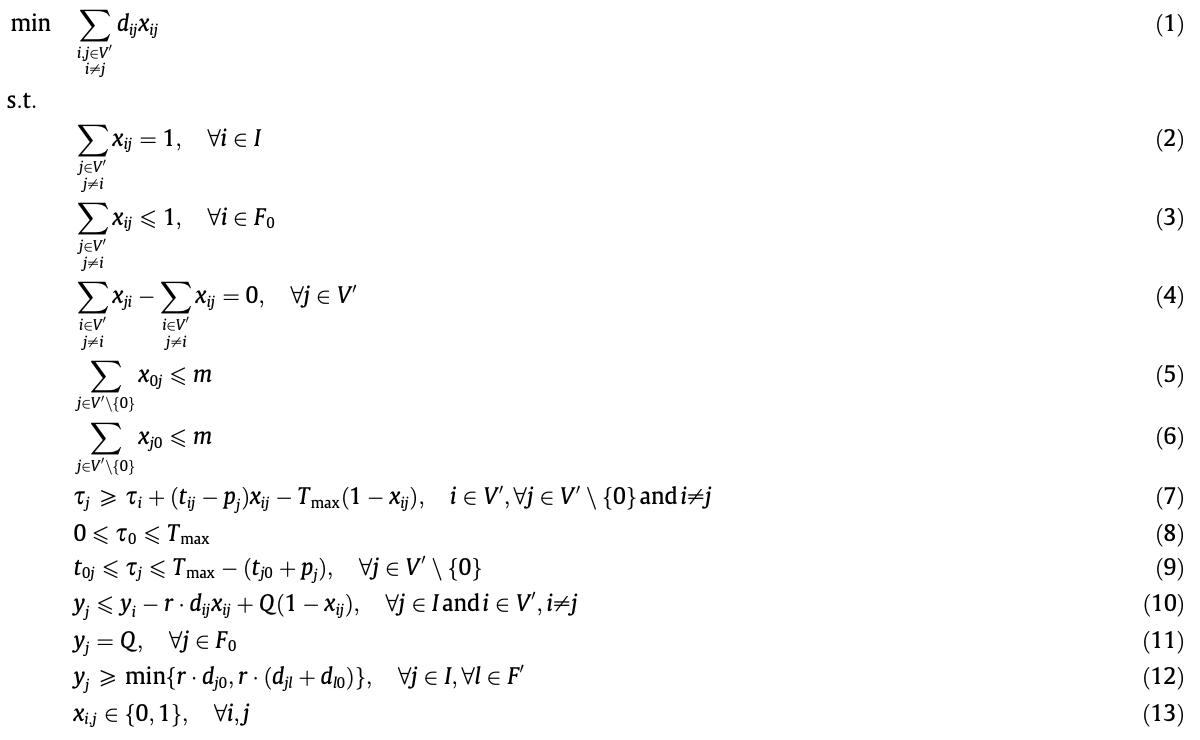
G-VRP 수리모형 대한 설명
- (1) : 차량들의 총 거리의 합을 최소화하는 것이 목적식이다.
- (2) : 각 고객 노드에서 나가는 차량은 정확히 하나다.
- (3) : 각 충전소 노드에서 나가는 차량은 1보다 클 수 없다.
- (4) : flow balance 제약식이다.
- (5),(6) : 최대 \(m\)개의 차량이 depot에서 출발하고 들어오도록 한다.
- (7) : 각 노드마다 차량이 이동하는 시간을 고려하여 도착시간을 부여한다. 여기서 왜 \(t_{ij} - p_j\)인지는 의문이다.
- (8),(9) : (7)번 제약식과 함께 각 차량이 \(T_{max}\)시간 전에 depot으로 돌아오도록 한다.
- (10) : 차량이 이동하면 연료를 차감시키는 역할을 한다.
- (11) : 차량이 depot나 AFS에 도착하면 연료 상태를 최대상태\(Q\)로 만들어준다.
- (12) : depot로 돌아오기 위해 충분한 연료가 있어야 하도록 한다. 이 제약으로 차량이 오도가도 못하는 상황을 방지한다.
- (13) : binary variable에 대한 제약이다.
보통의 VRP에서는 subtour을 방지하는 제약식을 넣어주어야 하는데, 이 경우에는 (7)~(9)번 제약을 통해 subtour이 자연적으로 사라지게 된다. 도착 시간이 더 짧은 노드로 다시 갈 수가 없기 때문이다.
G-VRP에 대한 휴리스틱 기법
MCWS Heuristic
MCWS는 전통적인 VRP문제를 푸는 휴리스틱 알고리즘은 Clarke and Wright Sacings 알고리즘을 G-VRP에 맞게 변형시킨 것이다. 구체적인 알고리즘은 다음과 같다.


MCWS가 끝나면 앞서 보았던 수리모형의 (5),(6)번 제약식이 relaxation된 상태로, 차량의 수와 관련된 제약이 없는 feasible solution을 얻을 수 있다. 알고리즘은 feasible tour list에 있는 tour들이 더이상 merge될 수 없을 때까지 진행되는데, 최종 솔루션에서 tour의 개수는 step5에서 merge하는 과정을 통해 최대한 작은 값을 얻게 된다. 즉, 최종 tour의 개수가 \(m\)보다 크다면 \(m\)대의 차량으로 모든 demand를 커버하지 못한다는 것이다.
보통의 VRP문제들의 솔루션은 사이클이 없는 형태이지만, G-VRP에서는 충전소를 여러번 방문할 수 있기 때문에 사이클 형태가 나올 수 있다. 다음 예시를 보자.
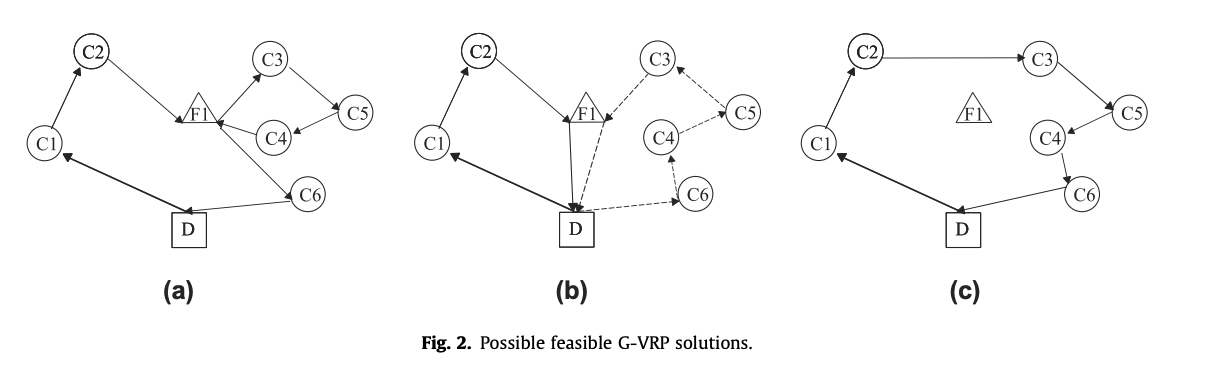
(a)번을 보면, F1충전소를 두번 지나가면서 사이클을 만든 것을 볼 수 있다. 그리고 (b)를 보면, 두대의 차량이 각각 한번씩 하나의 충전소를 두번 방문한다. 그리고 (c)와 같이 아무 차량도 충전소를 방문하지 않을 수 있다.
다음 그림은 Merging과정이 어떻게 문제에 영향을 미치는 지 보여준다.
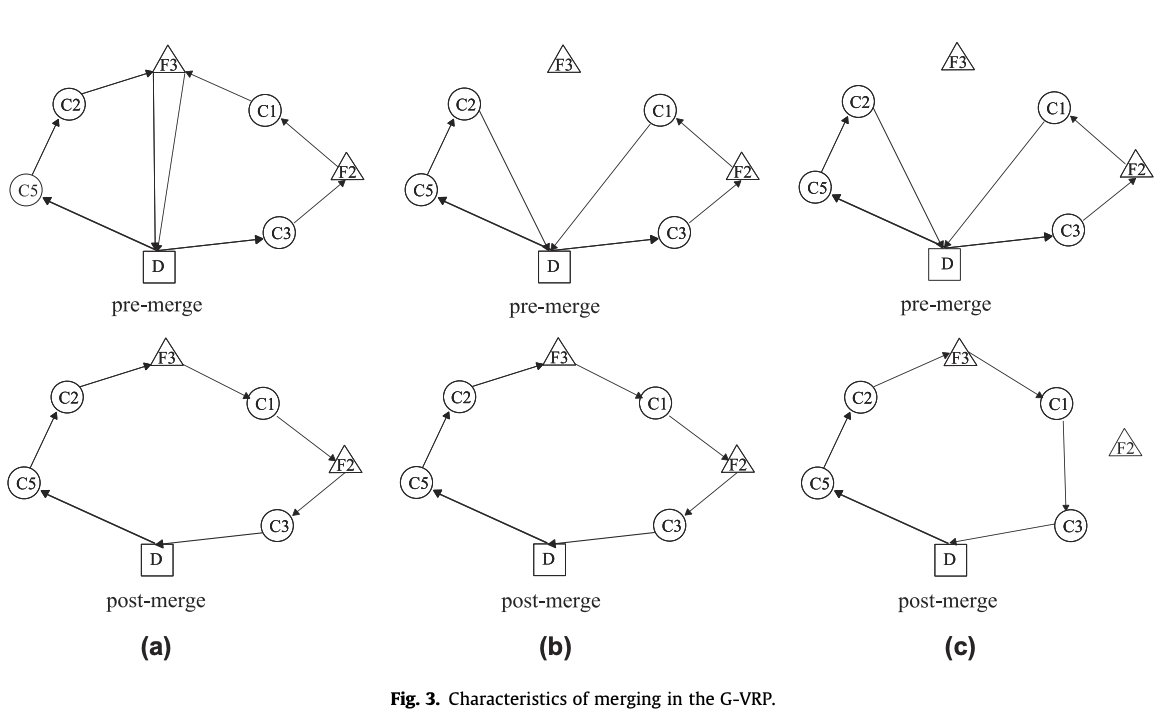
(a)를 보면, 같은 충전소를 지나는 두개의 tour는 depot에 갈 필요 없이 서로 연결(merge)시켜 하나의 tour로 만들어 줄 수 있다. 이때는 새로운 아크를 연결할 필요도 없다.
(b)를 보면, 어떤 경우에는 직접적으로 merge할 수 없던 tour들도 merge가 가능하다는 것을 볼 수 있다. 이와 같이 추가적인 AFS를 방문하는 것을 포함하는 merge는 기존 tour에서 방문하던 AFS를 방문할 필요가 없어질 수도 있다.
(c)를 보면, 기존에 방문했던 AFS를 방문하지 않고 다른 AFS를 지나는 경우가 생기기도 한다.
DBCA Heuristic
DBCA는 Density Based Spatial Clustering of Applications with Noise(DBSCAN) 알고리즘을 이용해서 큰 공간에서 클러스터를 찾고, 클러스터 내부를 연결하는 경로와 클러스터 외부를 연결하는 경로를 각각 찾는 방법이다.
DBCA의 핵심 아이디어는 주어진 반경안에 있는 이웃에 적어도 일정 수 이상의 노드가 있어야 한다는 것이다. 다음 그림은 20개 고객노드와 3개의 AFS를 가진 경우에 대해서 DBCA방법을 적용한 예시이다.
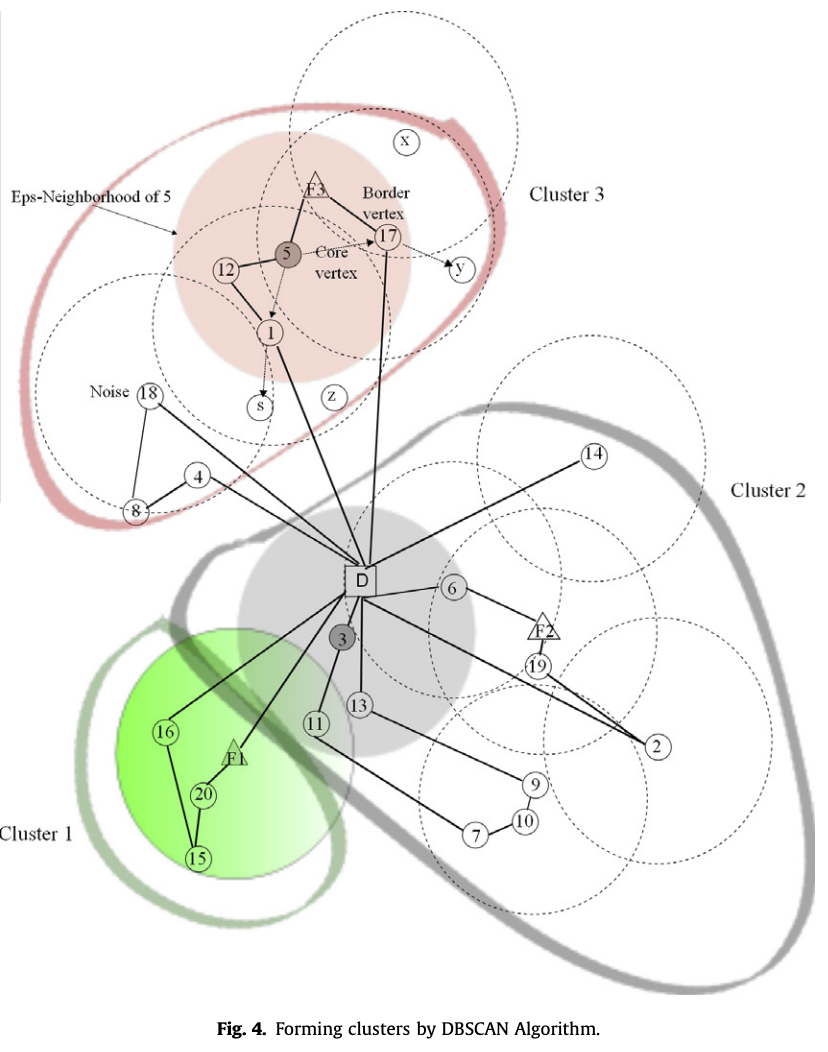
DBCA의 구체적인 절차는 다음과 같다.

먼저 일반적인 클러스터링을 한 후, 클러스터 안에 있는 고객들에 대해서 한 차량으로 serve를 하고 클러스터들은 차량 capacity가 넘지 않도록 한다. 하지만 DBCA에서는 클러스터들이 그러한 제약들에 대한 고려가 없기 때문에 앞서 본 예시에서 처럼 한 클러스터 내에서 여러개의 tour를 만들 필요성도 있다.
improvement heuristic
MCWS heuristic이나 DBCA는 feasibe tours를 만들지만 이보다 더 나아가서, 총 주행거리를 줄일 수 있는 방법들을 적용할 수 있다. inter-tour vertex exchange, within-tour two-vertex interchange & reordering등을 G-VRP에 맞게 변형시켜 사용될 수 있다.
inter-tour vertex exchange란, 각 tour쌍에 대해서 두개의 vertex가 선택되어 위치를 바꿔주는 것이다. 만약 총 이동거리가 줄어들고 제약을 모두 만족한다면 교환이 이루어진다.
within-tour vertex interchange & reordering은 모든 노드 쌍에 대해서 교환해보는 것이다. 선택된 두개의 노드의 위치가 바뀌고, 새로운 tour순서가 생긴다. 만약 새로운 투어가 제약을 만족하지 못한다면 노드 교환을 하지 않는다. 만약 만족한다면 AFS redundancy를 확인한 후 AFS의 위치를 바꿀 수 있다.
실험결과
G-VRP문제에 대한 작은 랜덤 데이터를 만들어서 exact solution과 heuristic solution을 비교해보았다. 그리고 현실적인 G-VRP문제에 대한 실험으로 버지니아의 의학용품 공급회사를 depot로 삼고 버지니아, 매리랜드, 컬럼비아의 병원들을 고객으로 삼는 네트워크를 만들어 실험을 진행했다.
작은 랜덤 데이터에 대한 실험결과
먼저 다음과 같은 시나리오들에 대한 실험을 진행했다.

그리고 랜덤한 데이터인 시나리오1에 대한 실험결과는 다음과 같았다.
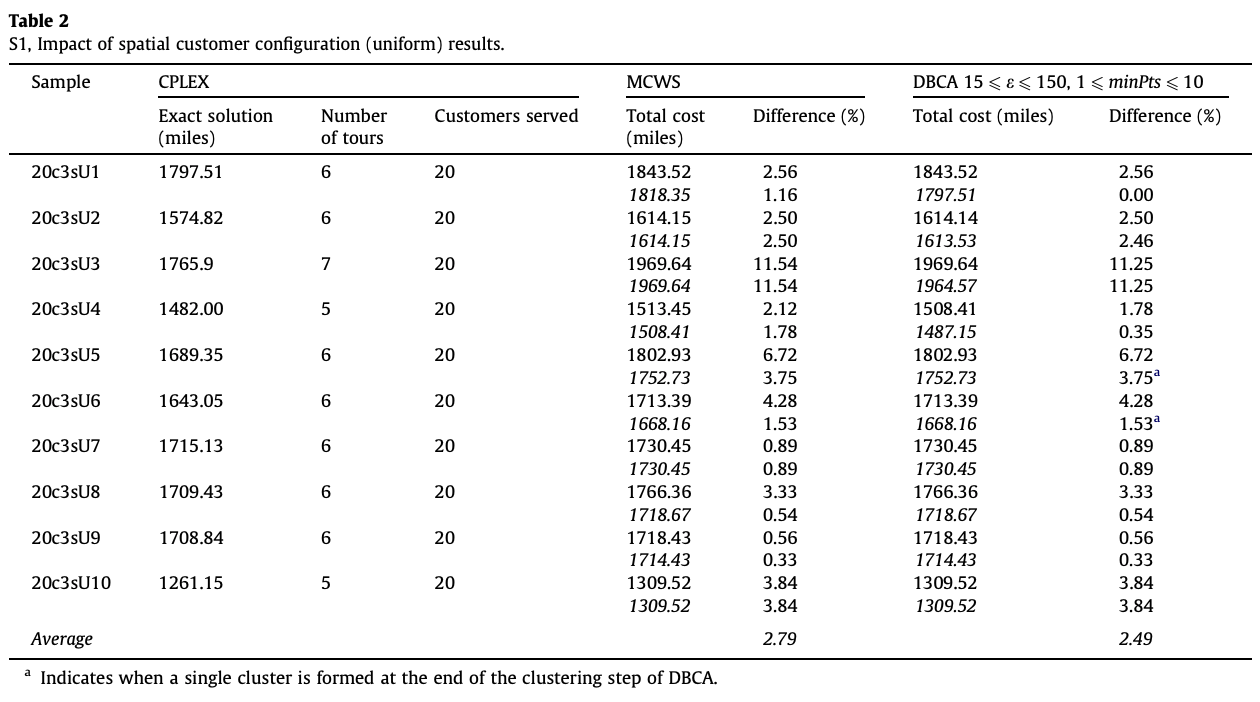
클러스터가 있는 데이터인 시나리오2에 대한 실험결과는 다음과 같았다.
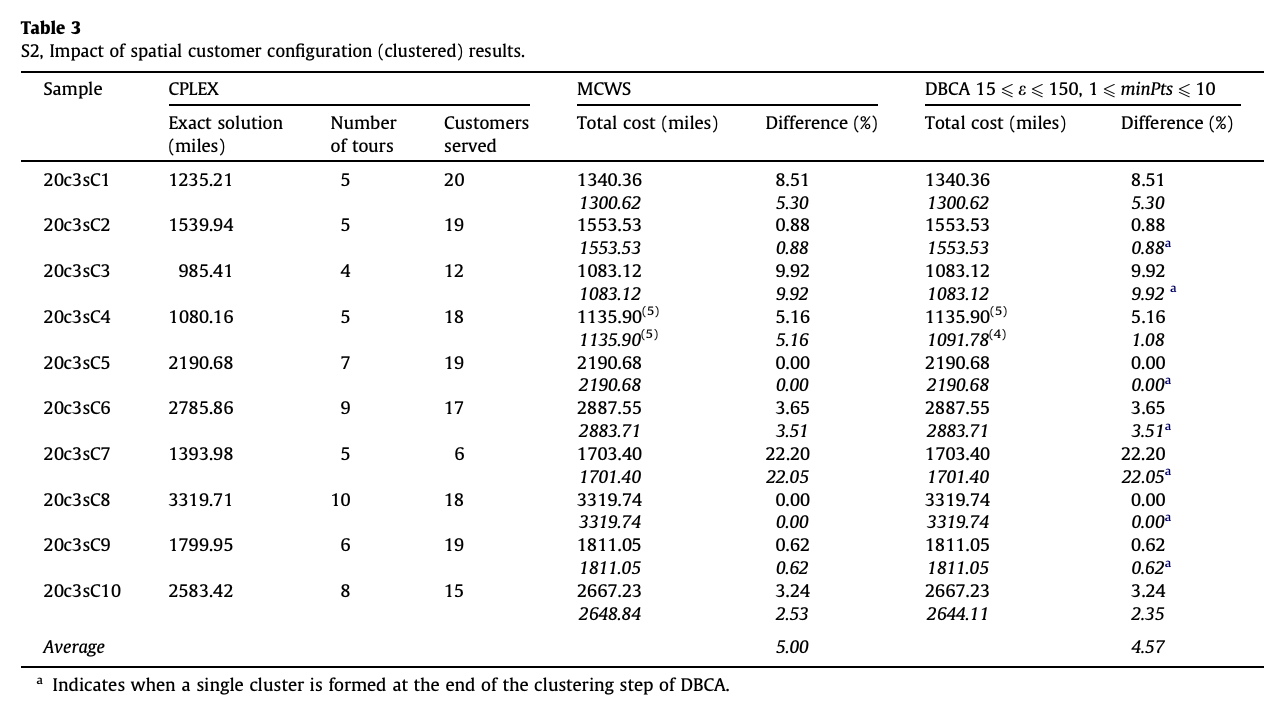
시나리오 1,2의 데이터를 섞고 충전소의 개수를 늘린 데이터인 시나리오3에 대한 실험결과는 다음과 같았다.
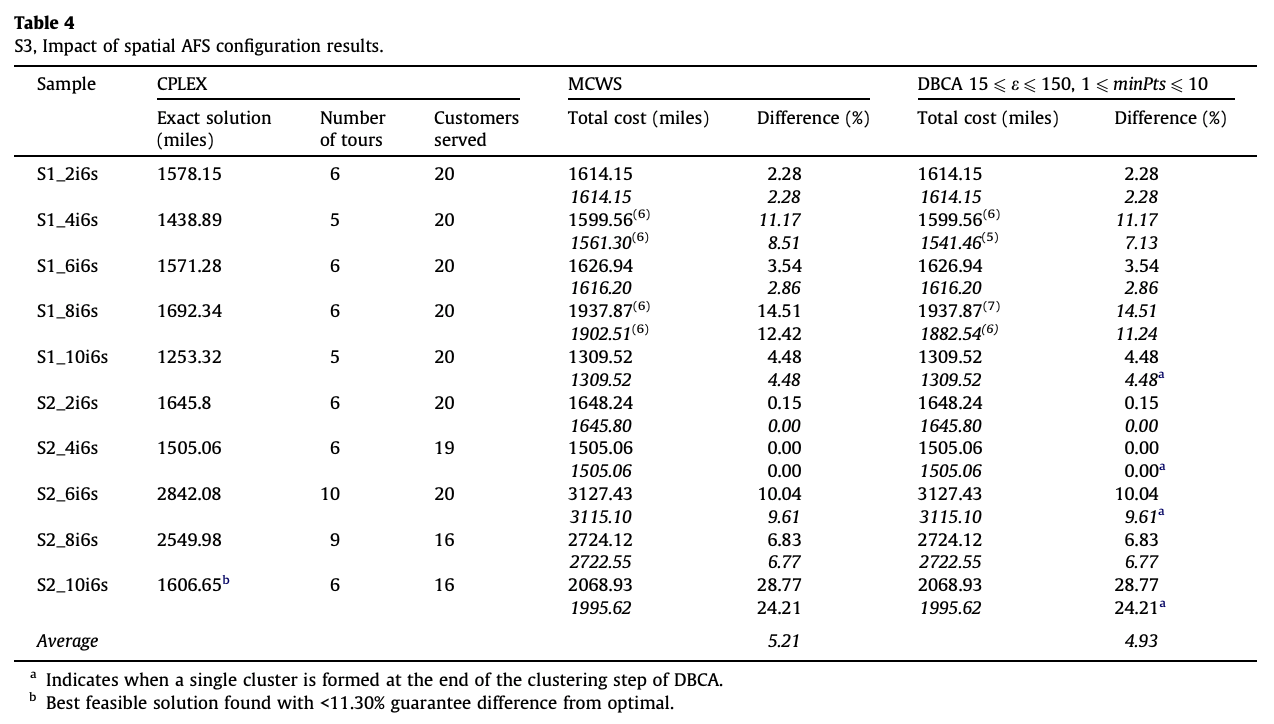
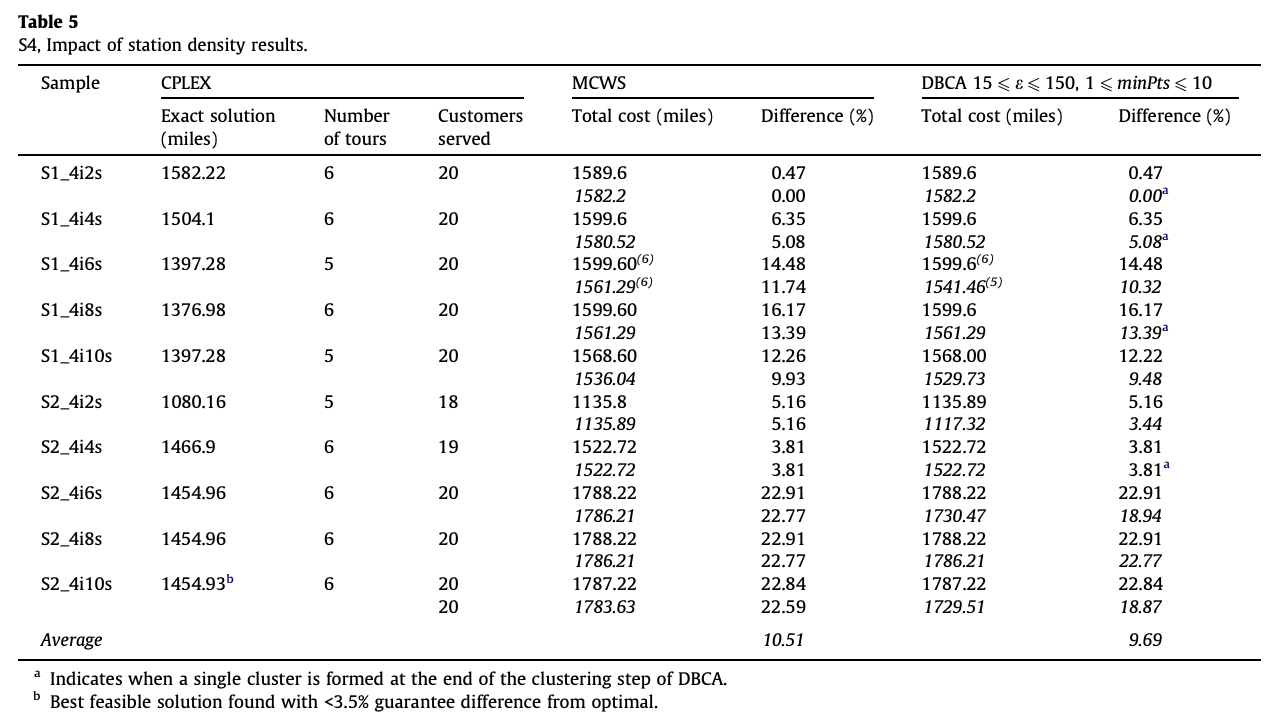
시나리오 1,2의 데이터를 섞고 충전소의 개수를 점점 늘려가면서 실험한 시나리오4에 대한 실험결과는 다음과 같았다.
현실 데이터에 대한 실험결과
현실 데이터에서는 다음과 같은 시나리오들을 통해 실험을 진행했다.

시나리오 1,2에 대한 결과는 다음과 같다.
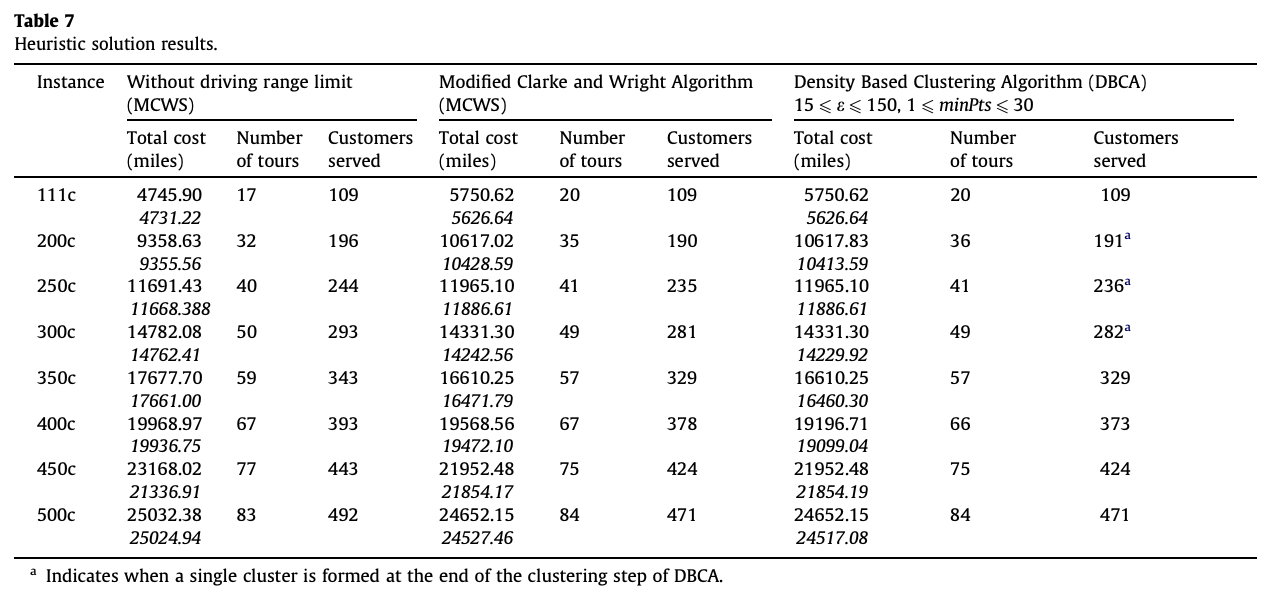
시나리오 3에 대한 결과는 다음과 같다.
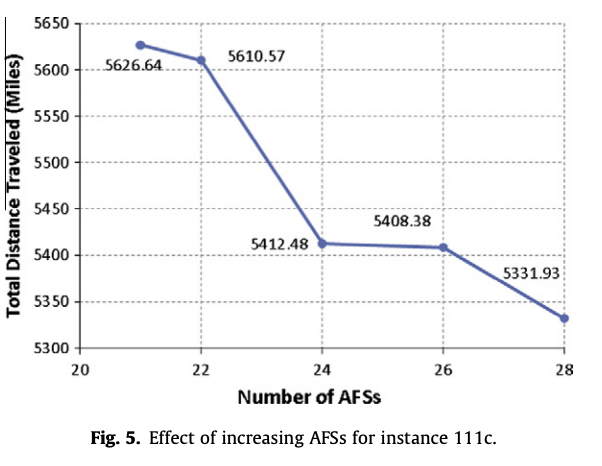
시나리오 4에 대한 결과는 다음과 같다.
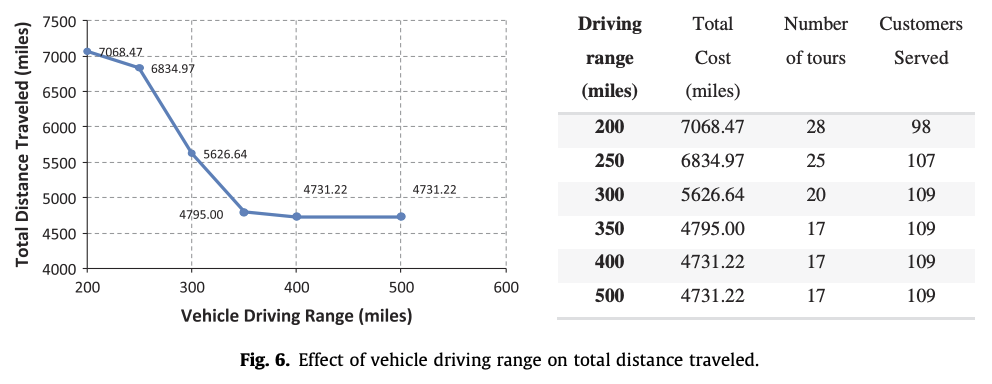
결론
- 이 논문은 G-VRP에 대한 수리모형과 휴리스틱 기법을 소개했다.
- 휴리스틱 기법들은 exact solution에 비교될만큼 문제를 잘 풀어냈다.
- 이러한 기법은 기업들에게 있어 차량의 운행경로를 제공할 뿐아니라 차량의 대수를 늘리거나 고객의 수를 감소시키는 등의 의사결정에도 도움이 될 수 있다.
- 현실적으로 규모가 큰 데이터를 이용해 실험을 진행하여 휴리스틱 기법의 효용성을 알아보았다.
- 충전에 시간이 오래걸리는 전기차에서부터 일반적인 내연기관차량에 대해서도 제안된 방법을 이용해서 문제를 풀 수 있다.