이번 세미나 발표 논문은 Mitigate the range anxiety: Siting battery charging stations for electric vehicle drivers이다.
주제는 전기차 충전소 설치문제인데, 배터리에 대한 운전자의 불안감과 경로 우회를 최소화하도록 충전소를 설치하는 것이 주요 내용이다.
논문의 저자는 홍콩 폴리텍 대학교의 Min Xu, Hai Yang, Shuaian Wang이다.
연구 배경
전기차가 화석연료에 대한 의존성과 온실가스 배출 경감에 도움이 될 것으로 기대하고 있다.
그런데 사람들은 여러가지 이유로, 전기차를 구매하기를 망설인다.
그 주요 요인 중에 하나가 도착지에 가기 전에 전기가 바닥날 걱정(range anxiety)이다.
이러한 걱정을 줄이기 위해서는 충분한 충전 네트워크가 구축되어 있어야 한다.
전기차 충전소의 종류는 3가지로 나눌 수 있다.
- AC Level 1 : normal/slow charging station
- AC Level 2 : normal/slow charging station
- DC Level 3 : fast EV charging station
Level 1,2와 같은 일반 충전소는 충전시간이 오래걸리기 때문에 가정용으로 쓰기에 적합하고, 고속 충전을 지원하는 Level 3 충전소는 고속도로나 지하철 근처와 같은 공공 장소에서 사용하기 좋다.
그러나 고속충전소는 조달비용이나 설치비용이 매우 비싸다. 일반적으로 조달에는 $10,000~$40,000, 설치에는 $4000~$51,000이 든다고 한다.
그렇기 때문에, 최적화된 방식으로 신중한 계획을 세울 필요가 있다.
관련 연구
전기차 충전소 설치 문제에 관한 연구
이 문제에 대한 연구가 꽤 많이 진행되고 있는데, EV 충전소는 보통 경로 중간에 위치한다는 점에서 demand를 네트워크의 origin-destination(OD) pair를 지나는 통행량으로 두고 모델링을 진행한다. 이와 관련된 것으로, 최대한 많은 flow를 capture하도록 하는 flow-capturing location model(FCLM)이 개발되었다.
그리고 FCLM이 확장되어 하나의 경로에 대해서 여러개의 충전소를 지나치는 것을 고려한 flow refueling location model(FRLM)이 개발되었다. 도착지에 무사히 도달하기 위해 충전소를 적절히 조합한다는 개념이 나오게 된 것이다.
그리고나서 FRLM이 다시 한번 확장되어 운전자들이 충전을 위해 우회하는 경우를 고려한 모델인 deviation-flow refueling location model(DFRLM)이 개발된다.
그리고 이러한 연구들을 통해 여러개의 충전소를 거치는 것에 대한 효용성에 대한 연구가 많이 진행되었다.
하지만 위 방법들은 OD pair에 대한 가능한 EV 충전소 조합과 우회 경로 조합을 미리 찾아야하는 문제들이고, 그러한 조합을 통해 문제를 푸는 것이 쉽지 않기 때문에 큰 사이즈의 문제에 대해서는 한계가 있다.
운전자들의 range anxiety에 대한 연구
그리고 EV 운전자들이 느끼는 range anxiety에 대한 경험적인 연구도 많이 진행되었다.
운전자들은 충전상태가 용량의 50%이하로 떨어지자마자 불안감을 느끼는 경우가 많은 것으로 나타났고,
데이터에 따르면, 배터리의 상태(SoC)가 운전자의 불안감에 비선형적인 영향을 미친다는 것을 발견했다.
그리고 EV의 기능들이 운전자들의 불안감에 영향을 많이 끼치는 것으로 나타났으나, 충전 기반시설들이 그러한 불안감을 줄여준다는 것을 발견했다. 그리고 range anxiety는 배터리 용량이 어떤 시점에 도달했을 때 생기기 시작하는데, 이 용량을 comfortable range threshold라 부른다. 그리고 재충전에 대한 접근성(recharge accessibility)가 range anxiety에 중요한 요인이었다.
이외에도 다양한 연구가 진행된 바 있다.
EV 충전소 설치문제에 range anxiety가 고려되어야 하는 이유?
다음 그림를 보자. link 위에 적힌 퍼센트는 배터리 소비량을 나타내고있다.
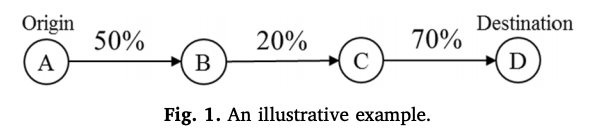
그리고 다음과 같은 가정이 있다고 하자.
- Origin에서 완충된 상태로 출발을 한다.
- 하나의 충전소를 지을 수 있다.
- comfortable range threshold는 30%이다.
이때, RFLM이나 DRFLM에서는 노드 B나 C에 충전소를 설치한다면 flow가 경로를 끝까지 할 수 있다.
하지만, 운전자의 불안감을 감안한다면, 노드 B에 충전소를 설치했을 때 노드 C에서 노드 D로 가는 동안 배터리의 상태가 10%까지 떨어지기 때문에
노드 B보다는 노드C에 설치하는 것이 더 좋은 선택이다.
이러한 이유로, range anxiety는 EV 충전소 설치문제에 충분히 고려될 만하다.
논문의 목적
이번 논문은 운전자의 range anxiety와 우회 경로를 고려하여 도시간의 이동에 대한 EV급속충전소 설치 문제를 풀고자 한다.
그리고 논문에서는 다음 몇가지 가정을 한다.
- 먼저 EV는 제한된 주행거리를 가지고 있다.
- 운전자의 불안감은 EV 배터리 잔여량에 의해 nonlinear하게 변화한다.
- 운전자는 충전을 위해 OD-pair의 최단경로를 벗어나서 이동하기도 한다.
이러한 가정하에, 논문은 제한된 예산 내에서 전체 운전자의 range anxiety를 최소화하는 충전소의 위치를 구하는 것을 목적으로 한다.
이를 위해, 논문에서는 미리 경로에 대한 조합을 미리 계산하는 FRLM이나 DFRLM의 방법을 벗어나서 충전 방식과 경로 우회에 대한 것을 직접 명시하는 MIP모델을 만든다.
하지만 range anxiety가 비선형이기 때문에 이는 non-linear모델이고, 이는 solver로 쉽게 풀수는 없다.
그래서 논문에서는 허용오차 \(\epsilon\)을 도입하여, optimal에 오차를 의미하는 \(\epsilon\)-optimal solution을 효율적으로 얻는 방법을 제안한다.
가정과 notation
먼저 논문에서는 다음과 같은 notation을 사용한다.

그리고 논문은 다음과 같은 가정을 둔다.
- EV충전소에 대한 후보지 노드에만 충전소를 설치할 수 있다.
- 출발지에서의 배터리 양과 도착지에서의 배터리 양은 미리 지정한 각각의 기준을 따른다.
- 충전소에서 충전을 할 시 완충을 한다.
- 충전소에는 용량 제약이 없다.
- 미리 정해놓은 오차범위 내에서, 운전자들은 최단경로를 우회해서 충전을 한다.
- 운전자들은 여러개의 충전소를 거칠 수 있다.
Charging Logic
먼저 두개의 binary decision variable \(y_i\)와 \(x^w_{ij}\)를 정의한다.
\(y_i\) : \(i\) 지역에 충전소를 설치할 것인지
\(x^w_{ij}\) : OD pair \(w\)에 노드\(i\)에서 노드\(j\)로 가는 flow가 존재 하는지
그리고 continuous variable \(e^w_i\)을 정의한다.
\(e^w_i\) : 노드 \(i\)를 지난 직후의 배터리 잔여량
그리고 일반적인 네트워크에 대한 충전 로직을 포뮬레이션하기위해 다음 그림과 같은 네트워크를 사용한다.
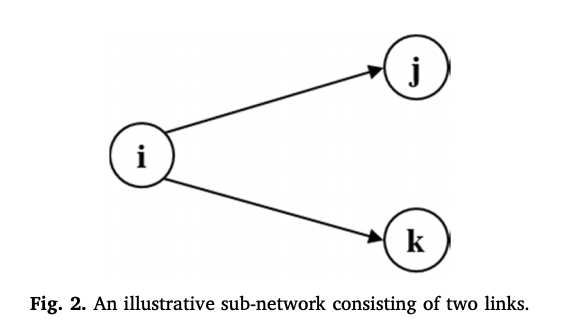
-
이때 기본적으로 link \(i,j\)간의 거리가 현재 배터리의 용량보다 크다면, 갈 수 없다.
\[e^w_i \geq d_{ij}x^w_{ij}\] -
그리고 만약 다음 노드\(j\)에 충전소가 설치되어 있다면, 배터리 용량이 최대 \(E\)가 된다.
\[e^w_j = E\] -
만약 다음 노드에 충전소가 있지만, 그 노드로 가지 않을 경우, 어떤 제약도 존재하지 않는다.
\[0 \leq e^w_j \leq E\] -
그리고 다음 노드에 충전소가 없는데 그쪽으로 간다면, 배터리 용량이 줄어들게 된다.
\[e^w_j = e^w_i - d_{ij}\] -
다음 노드에 충전소가 없고, 그쪽으로 가지 않는다면, 이 역시 제약이 존재하지 않게 된다.
\[0 \leq e^w_j \leq E\]
앞서 나온 제약들을 통합하여 제약을 한번에 표현해주어야 하는데, 이때 3,5번은 아무 제약식이 아니기 때문에 2,4번을 합쳐야 한다. 특히 3,5번 제약을 위반하지 않고 2번 제약을 표현하기 위해서는 다음 식을 만들 수 있다.
\[Ey_j \leq e^w_j \leq E\]그리고 2,3,5번 제약을 위반하지 않고 4번 제약을 표현해주기 위해서 다음과 같은 제약식으로 바꿔줄 수 있다.
\[e^w_j \leq e^w_i - d_{ij} + Ey_j\]다음으로, 4번 제약의 \(e^w_i - d_{ij}\)가 음수가 되지 않게 하기 위해서, 새로운 항 \(d_{ij}(1-x^w_{ij})\)를 추가해준다. 그리고 5번 제약을 위해서 \(E(1-x^w_{ij})\)를 추가해준다.
\[e^w_j \leq e^w_i - d_{ij} + Ey_j + d_{ij}(1-x^w_{ij}) + E(1 - x^w_{ij})\]이를 정리하면 다음 식이 나오게 된다.
\[e^w_j \leq e^w_i - d_{ij}x^w_{ij} + E(1-x^w_{ij}+y_j)\]최종적으로 충전에 대한 1~5번 제약은 다음 두 식으로 정리할 수 있다.
\[\begin{cases} Ey_j \leq e^w_j \leq E\\ e^w_j \leq e^w_i - d_{ij}x^w_{ij} + E(1-x^w_{ij}+y_j) \end{cases}\]Driving range anxiety
앞서 언급한 선행 연구에 따르면, 다음과 같은 연구가 있었다.
- Range anxiety는 잔여 배터리 용량에 큰 영향을 받는다.
- EV 운전자들이 range anxiety에서부터 자유로운 구간(comforatble range threshold)이 존재한다.
- 배터리 상태(SoC)가 0에 가까워지면서 range anxiety는 높아지고, 변화량 역시 증가한다.
이러한 연구에 따라 논문에서는 다음 가정을 둔다.
- EV 운전자의 range anxiety는 배터리 잔여량이 증가할 수록 최대값\(R_{max}\)부터 comfortable range threshold(\(E_{conf}\))까지 convex하게 떨어진다. 그리고 SoC가 최대량 \(E\)가 되면 range anxiety는 0이 된다.
다음 그림을 보면, SoC에 따른 EV운전자의 range anxiety의 변화량에 대한 그래프를 보여준다. SoC가 \(E_{conf}\)에 도달하기까지 그 변화량이 점점 줄어드는 것을 볼 수 있다.
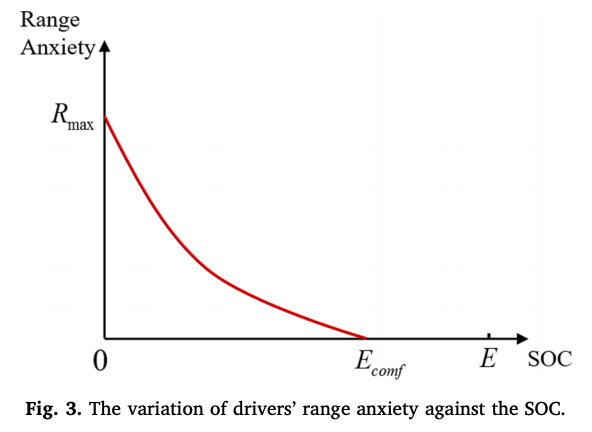
그리고 다음 그림을 보면, 일정한 속도로 운전했을 때 배터리의 상태는 선형적으로 줄어들고, SoC가 \(E_{conf}\)보다 낮아졌을 경우 다시 충전될 때 까지 range anxiety가 convex하게 증가하는 것을 볼 수 있다. 완충된 경우 다시 range anxiety는 0이 된다.
그리고 논문에서는, 선형적인 SoC에 대한 함수를 \(S(t)\), convex한 range anxiety에 대한 함수를 \(R(t)\)라고 둔다.
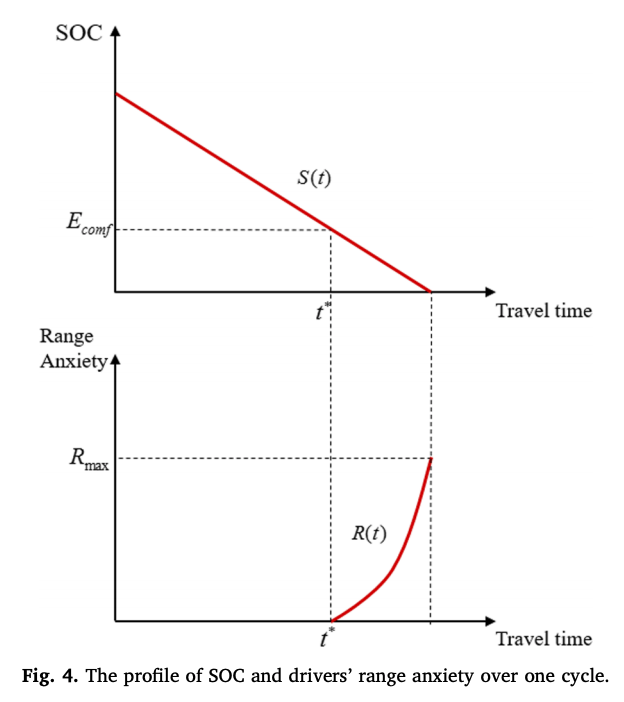
그리고 다음 그림은 전체 주행중 배터리의 상태와 range anxiety를 나타낸다.
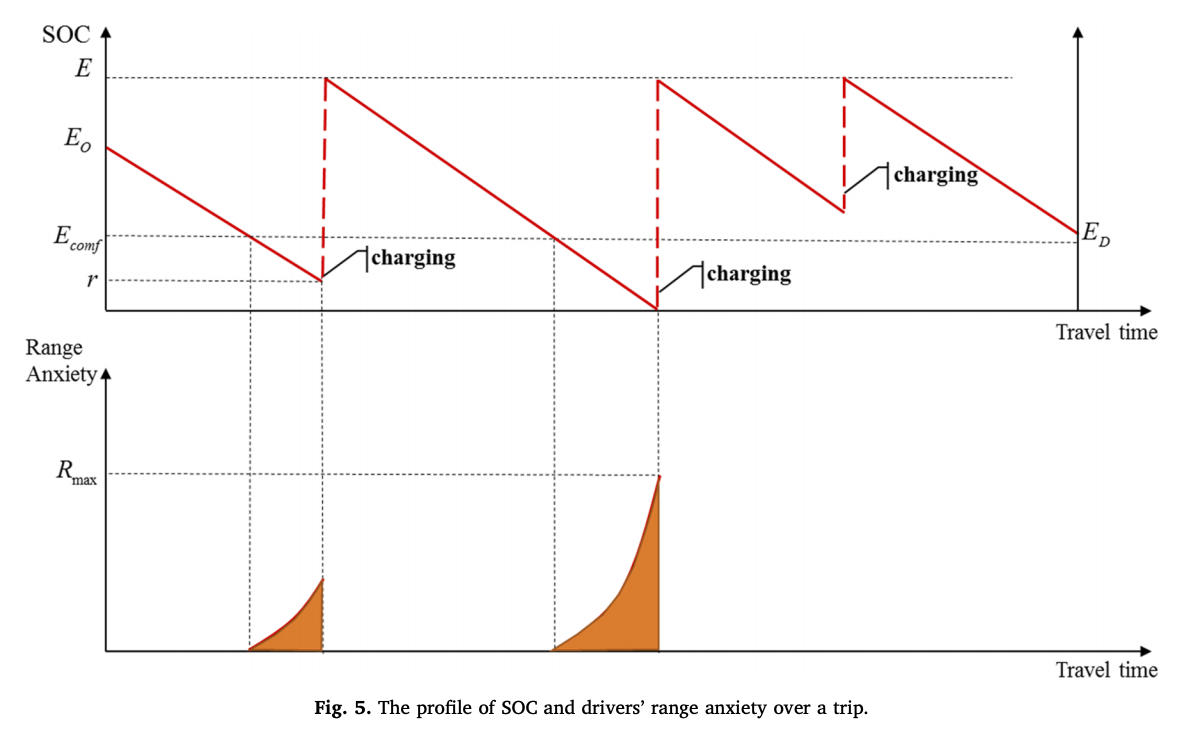
그리고 모델을 만들기 위해서 origin부터 첫 충전소까지, 두개의 붙어있는 충전소, 마지막 충전소부터 destination까지의 경로를 각각 쪼개서 sub-path를 만든다. 그리고 마지막 sub-path의 마지막 노드에서의 최종 SoC를 \(r\)이라고 한다. 이때 위 그림에서 주황색 부분은 다음 식에 의해 계산될 수 있다.
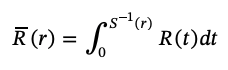
각 sub-path들은 충전소 혹은 도착지인 마지막 노드로 구분되기 때문에 우리는 각 sub-path들에 대한 range anxiety의 합으로 전체 경로에 대한 range anxiety를 표현할 수 있다. 정확히 말해서, \(r^w_j\)를 OD pair \(w\)에서 차량이 충전소나 도착지 \(j\)에 도착했을 때의 SoC라고 정의한다면, 앞서 유도한 제약을 이용해서 다음 식으로 나타낼 수 있다.
\[r^w_j \leq e^w_i - d_{ij}x^w_{ij} + E(1-x^w_{ij}), \forall (i,j) \in A, j \in I \cup \{s(w)\}, w \in W\]그리고 총 누적 range anxiety는 다음 식으로 표현된다.
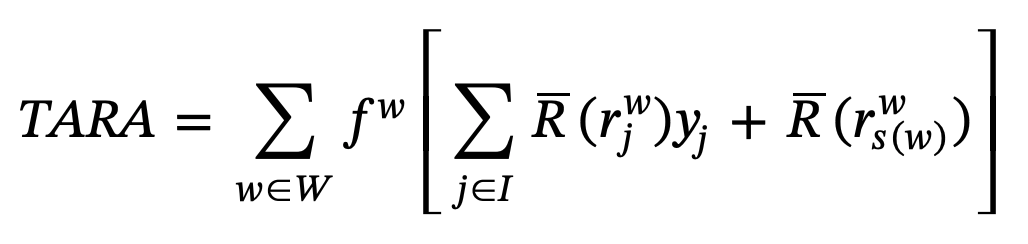
Optimization Model
주행거리나 예산의 한계로 인해서 충전을 할 수 없는 경우를 위해, 논문에서는 시작점과 도착점을 잇는 길이가 0인 추가적인 링크를 하나 만든다. 이 링크를 통해 갈 수 있게 하기 위해서 origin에서의 배터리 양이 destination에서의 배터리 양보다 크거나 같다면 이 링크를 갈때 소비되는 전기량을 0으로 설정하고 그 외의 경우에는 origin에서의 배터리양 - destination에서의 배터리 양으로 설정한다.
그렇게하여 만들어진 DSCP모델은 다음과 같다.

모델 설명
-
목적식은 총 range anxiety와 big-M의 총합을 minimize하는 것이다. 여기서 big-M은 cover되지 못한 demand에 대해서 패널티를 부여하는 것이다. 그렇기 때문에 big-M의 값은 충분히 커야한다.
- 14번 제약식은 각 OD pair에 대한 flow conservation 제약이다.
-
15번 제약식은 충전소 설치 비용이 예산을 넘지 못하게 하는 제약식이다.
- 16~18번 제약식은 앞 부분에서 설명한 charging logic에 대한 것으로, 16,17번은 차량이 지나가면서 SoC가 바뀌도록 하는 제약식이다.
- 16번 제약식은 차량이 이동하면서 배터리의 용량이 줄어드는 것을 표현했다.
- 17번 제약식은 충전소가 있는 곳에서 차량의 배터리가 완충되는 것을 표현했다.
-
18번 제약식은 현재 배터리 용량보다 큰 전기를 필요로하는 경로로는 갈 수 없도록 한다.
- 여기서 16번, 17번 제약식은 19번, 20번 제약식으로 축소될 수 있다.
-
그리고 21번 22번 제약식은 각각의 sub-path의 마지막 SoC의 상한을 정한다.
- 23번 제약은 우회하는 경로의 거리에 제약을 둔다.
-
24, 25번 제약은 출발할 때와 도착할 때 필요한 SoC에 대한 제약이다.
- 26, 27번 제약은 decision variable을 binary로 정의하는 제약이다.
모델의 특징
FRLM과 RFRLM모델은 미리 계산한 경로 조합을 통해 문제를 풀기 때문에 detour tolerance나 EV의 주행거리에 따라 문제 사이즈가 크게 바뀌고, 작은 네트워크에 대해서도 쉽게 문제를 풀 수 없는 반면, 이 모델은 polynomial 개수의 제약이 있고, 네트워크에 대해서 사이즈가 고정되어 있다.
그리고 모델 내에 charging logic과 range feasibility를 명시했기 때문에 미리 경로의 조합을 구할 필요가 없고, 실험 결과 메모리가 부족한 경우도 일어나지 않았다.
그리고 이 모델의 또 다른 장점으로, 충전소의 capacity나 다양한 주행거리를 고려한 특별한 문제에 대해서도 유연하게 문제를 풀 수 있다는 것이다. 예를 들어 목적함수를 바꿔서 flow를 maximize하는 문제로 바꿀 수도 있고, 예산을 설정하는 것 대신 cost를 부여해서 set covering 문제로 바꿀 수도 있다.
그런데, 이러한 장점이 있는 것은 사실이나 목적식에 \(\bar{R}(r^w_j)y_j\)와 같은 bilinear한 항이 존재하고, 적분 과정에서 nonlinear한 부분이 존재하기 때문에 쉽게 풀 수는 없다.
하지만 다행히, bilinear한 항은 다음과 같은 방식으로 선형화할 수 있다. 먼저 새로운 변수 \(Q^w_j\)를 만들고, 최적해에서 \(Q^w_j = \bar{R}(r^w_j)y_j\)가 되도록 다음 두 제약식을 추가한다.

여기서 \(\bar{R}_{max}\)는 sub-path에 대한 누적된 range anxiety의 최대값이다. 그리고 이와 같이 선형화를 한다면, 다음 proposition을 만족하게 된다.

\(S()\)는 선형적으로 감소하는 함수이기 때문에, 그 역함수인 \(S^{-1}()\) 역시 선형적으로 감소할 것이다. 즉, \(S^{-1'}(r) \geq 0\)이고 \(S^{-1''} = 0\)을 가진다. 그리고 \(R()\)은 증가하고, 미분가능하기 때문에, 우리는 \(R^{'}() \geq 0\)을 가진다. 그렇기 때문에 위 증명과 같은 \(\bar{R}^{''}(r) \geq 0\) 식이 나오게 되고, \(\bar{R}(r)\)이 convex함수임을 알 수 있게 된다.그렇기 때문에 논문의 모델 DCSP가 mixed-integer convex programming model임을 알 수 있게 되는 것이다.
Outer-approximation algorithm
The outer-approximation algorithm은 nonlinear한 부등식을 갖는 MIP문제에 대해 허용오차를 주고 \(\epsilon\)-optimal solution을 찾는 방법으로, 1986년 소개되어 여러 분야에서 사용된 바 있다.
이 알고리즘은 일반적인 convex한 nonlinear MIP를 풀 수 있게 하는데, 결과적으로 나오는 MILP는 cplex와 같은 상용솔버로 풀 수 있게 된다.
outer-approximation algorithm을 적용하기 위해서는 nonlinear한 \(\bar{R}(r^w_j)\)를 대신하는 \(B^w_j\)라는 continuous variable을 새로 만들고, 목적함수와 제약식에 넣어준다.
먼저 목적식은 다음과 같이 바꿔준다.
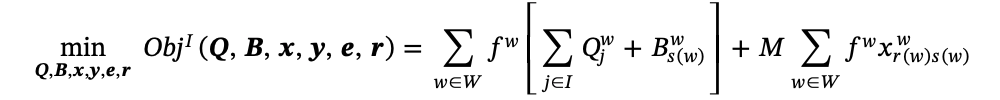
그리고 선형화 과정에서 생긴 제약식인 \(Q^w_j \geq \bar{R}(r^w_j) + \bar{R}_{max}(y_j-1)\)을 다음 식으로 바꿔준다.

여기서 \(B^w_j \geq \bar{R}(r^w_j)\)제약식은 다음 그림처럼 \(\bar{R}(r^w_j)\) 커브의 접선이 되는 많은 선형 함수로 대체하여 완화할 수 있다.
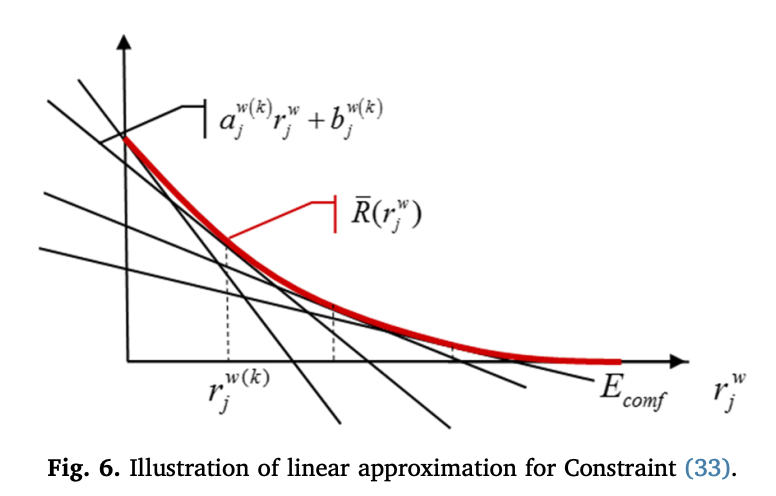
이러한 선형함수들은 과소평가된 range anxiety로 해석될 수 있고, 하나의 집합 \(K = \{1,2,...,K-1,K\}\)로 표현될 수 있다.
\(a^{w(k)}_j\)와 \(b^{w(k)}_j\)를 \(\bar{R}(r^w_j)\)의 k번째 접선의 기울기와 절편이라고 하자. 이때 \(B^w_j \geq \bar{R}(r^w_j)\) 식은 다음과 같이 표현될 수 있다.

\(a^{w(k)}_j = \bar{R^{'}}(r^{w(k)}_j)\)이고, \(b^{w(k)}_j = \bar{R^{'}}(r^{w(k)}_j) - \bar{R^{'}}(r^{w(k)}_j)r^{w(k)}_j\)이고, 결과적으로 다음과 같은 MILP 모델이 만들어진다.
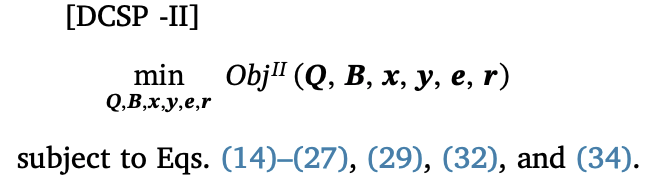
이 모델의 경우에는, 목적함수의 \(Q^w_j\)와 \(\bar{R}(r^w_{s(w)})\)가 과소평가되었기 때문에 원래 문제의 relaxation문제라고 볼 수 있다. 그렇기 때문에 이 문제는 다음 proposition에서와 같이, 원래문제의 lower bound를 제공한다.

\(\bar{R}(r^w_j)\)에 대한 piecewise linear approximation function을 다음과 같이 정의하자
\[\hat{R}(r^w_j) = max_{k \in K}\{a^{w(k)}_j r^w_j + b^{w(k)}_j\}\]이때 optimal solution에 대한 error는 \(\epsilon\)에 의해 몇개의 접선이 생길 것인지 정해지면서 조절된다. 즉, 만약 \(\bar{R}(r^w_j) - \hat{\epsilon} \leq \hat{R}(r^w_j) \leq \bar{R}(r^w_j)\)를 만족한다면, 우리는 다음 부등식을 얻을 수 있다.
\[Obj(x^*,y^*,e^*,r^*) - Obj^{\mathrm{II}}(Q^*, B^*, x^*, y^*, e^*, r^*) \leq \epsilon \qquad(37)\]그리고 다음 proposition을 통해 우리는 36,37번 식으로 \(\epsilon\)-optimal solution을 얻을 수 있다는 것을 알 수 있다.

convex function \(\hat{R}(r^w_j)\)을 \(r^w_j \in [r^{w(L)}_j, r^{w(U)}_j]\)의 domain에 대해 근사하기 위해서 주어진 허용오차 \(\epsilon\)에 대해서 접점의 집합을 \(E = \{r^{w(k)}_j, k \in K\}\)라 할 수 있고, 이 접점의 집합을 다음 알고리즘으로 구할 수 있다.
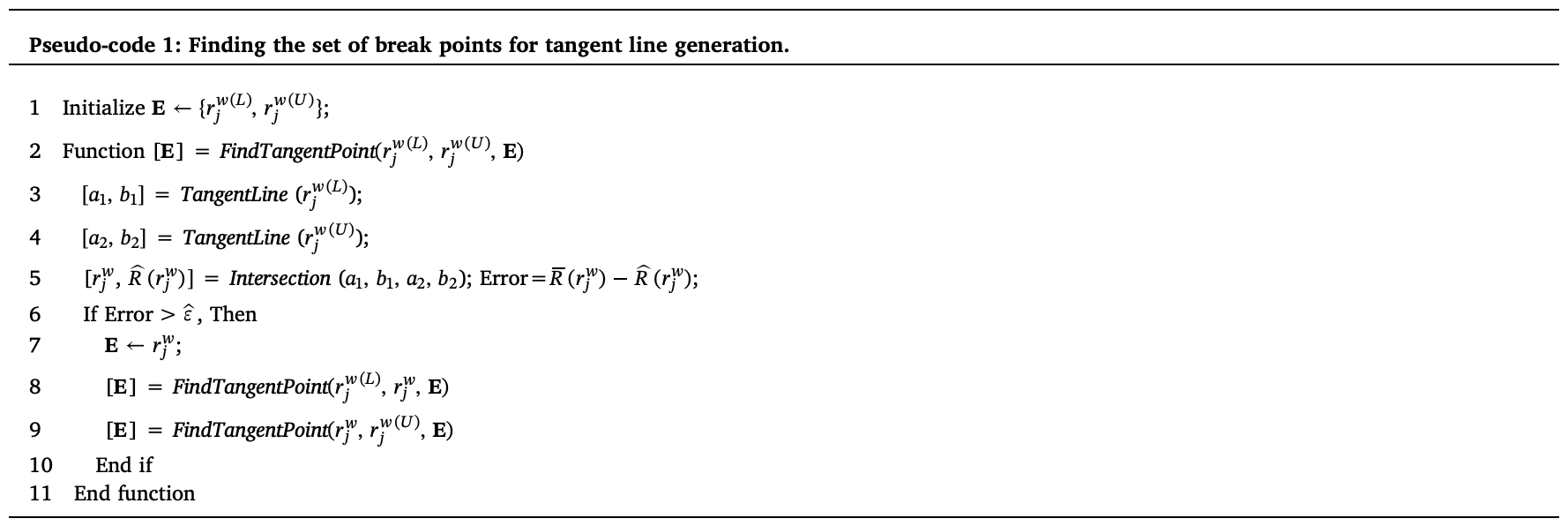
pseudo-code를 보면, FindTangentPoint는 접점을 찾기위한 재귀함수이다.
각각의 재귀 단계에서, 함수는 \([r^{w(L)}_j, r^{w(U)}_j]\) domain에 대한 접점과 에러를 반환한다.
TangentLine은 부수적인 함수로, 접선의 기울기와 절편을 반환한다.
Intersection은 두 직선의 교차점의 좌표를 반환한다.
이때 \(r^w_j \in [E_{conf}, E]\)인 경우, 즉 충분히 배터리 용량이 큰 경우 불안감 \(\bar{R}(r^w_j)\)이 0이기 때문에 접점을 \(r^w_j \in [0, E_{conf}]\)에 대해서만 구해준다.
Model Extension
이때까지의 모델은 RFLM과 DRFLM을 직접적으로 확장하여 range anxiety를 고려한 EV 충전소 설치 문제를 푸는 것이었다.
여기서 추가적으로, 충전을 하기 위해 기다리고, 멈춰야 하는 비용을 고려해줄 수 있다.
그러기 위해서 각각의 OD pair에 대해서 새로운 binary decision variable \(y^w_i, \forall i \in I, w \in W\)을 정의한다.
이 변수는 운전자가 OD pair \(w\)의 충전소 \(i\)에서 충전을 하는지에 관한 것이다.
charging impedance를 고려하여 충전소 위치를 선정하는 문제인 DCSPCI는 원래 문제의 13,16,17번 제약의 \(y_i\)를 \(y^w_i\)로 바꾸고, 23번 제약식의 좌변에 총 charging impdedance를 더해주고, \(y^w_i\)와 \(y_i\)를 연결시켜주는 제약을 추가하여 포물레이션 할 수 있다.
논문에서는 일반적인 charging impedance로 charging-amount-independent와 charging-amount-dependent 두가지 요소를 고려했다. 특히 \(i\) 충전소에서의 평균 charging impedance를 뜻하는 \(\alpha_i\)와 충전소 \(i\)에서 충전 단위마다 발생하는 charging-amount-dependent impedance를 의미하는 \(\beta\)를 이용해서 23번 제약식에 다음 항을 추가한다.
\[\sum_{i \in I}[\alpha_i y^w_i + \beta_i(E-r^w_i)y^w_j]\]이로 얻어지는 최종적인 수리모형은 다음과 같다.
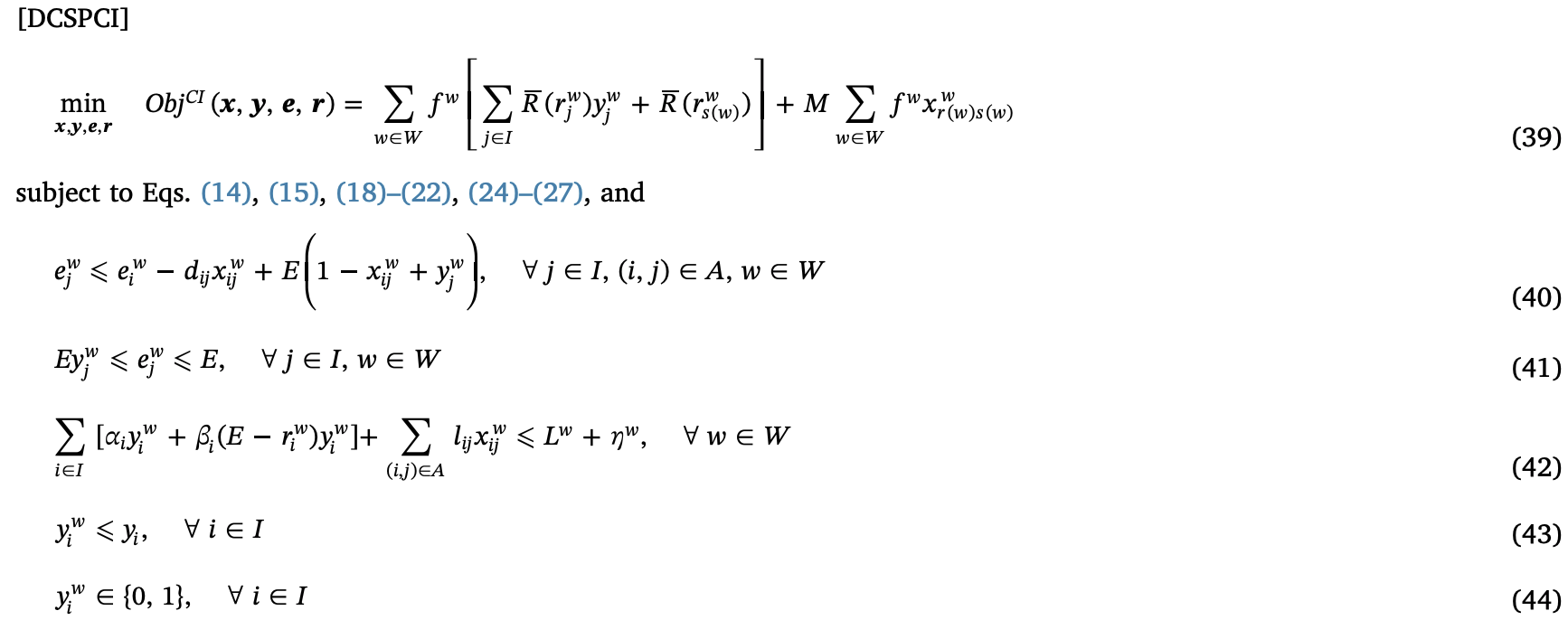
42번 제약에서는 charging-amount-impedance가 들어갔으며, 이는 bilinear하다. 원래 문제에서 bilinear을 없앤 것과 같이, 새로운 변수 \(P^w_i, \forall i \in I, w \in W\)를 이용해서 43번 제약식의 \((E - r^w_j)y^w_i\)를 대체할 수 있다. 그리고 다음 식으로 최적해에서 \(P^w_i = (E - r^w_j)y^w_i\)가 성립하도록 강제할 수 있다.


그리고 이 경우에도 proposition 1은 여전히 유효하기 때문에, 앞서 소개한 outer-approximation algorithm을 여기서도 사용할 수 있다. 따라서 DCSPCI에 대한 \(\epsilon\)-optimal solution을 다음 MILP 모델을 이용해서 구할 수 있다.
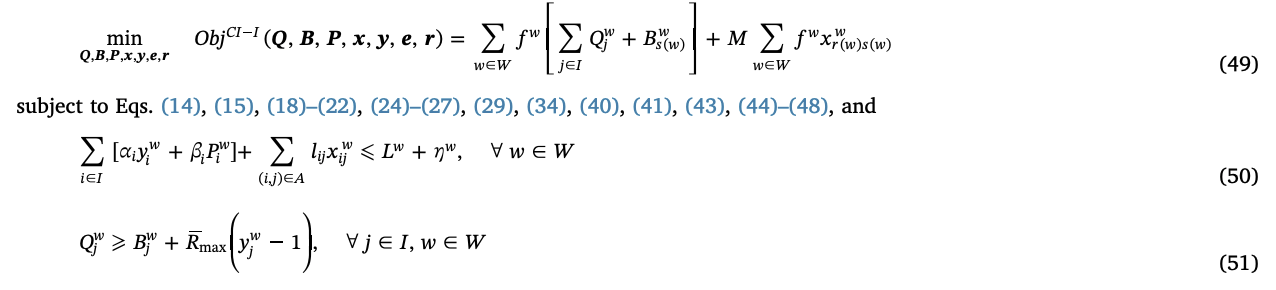
실험 결과
실험에는 25의 node를 가진 network와 현실의 Texas Highway network를 사용했다.
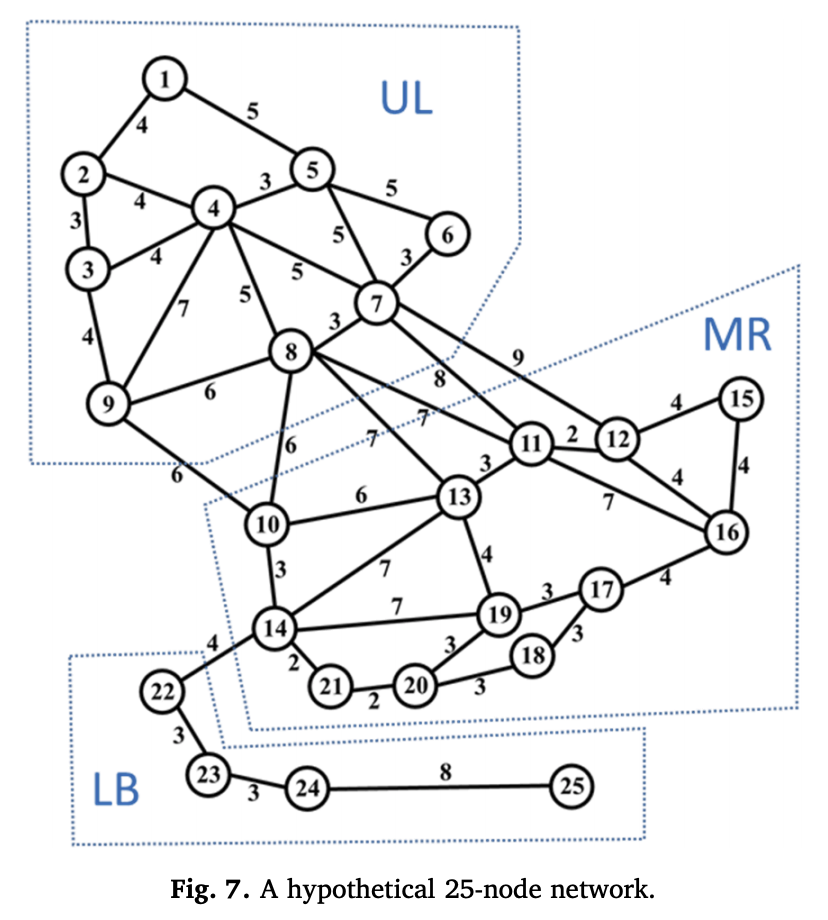
위 그림은 첫번째 실험에 사용한 네트워크이며 25개의 노드와 86개의 링크가 있다. 이때 링크(i,j)에 대한 전력소비량은 미리 정해놓은 정수 집합에서 랜덤하게 뽑아서 사용했다. 모든 노드가 출발지, 도착지, 충전소 후보지로 고려되었으며, 그 결과 300개의 OD pair와 25개의 후보지가 생겼다. 그리고 통행량은 gravity model을 따라서 만들었다.
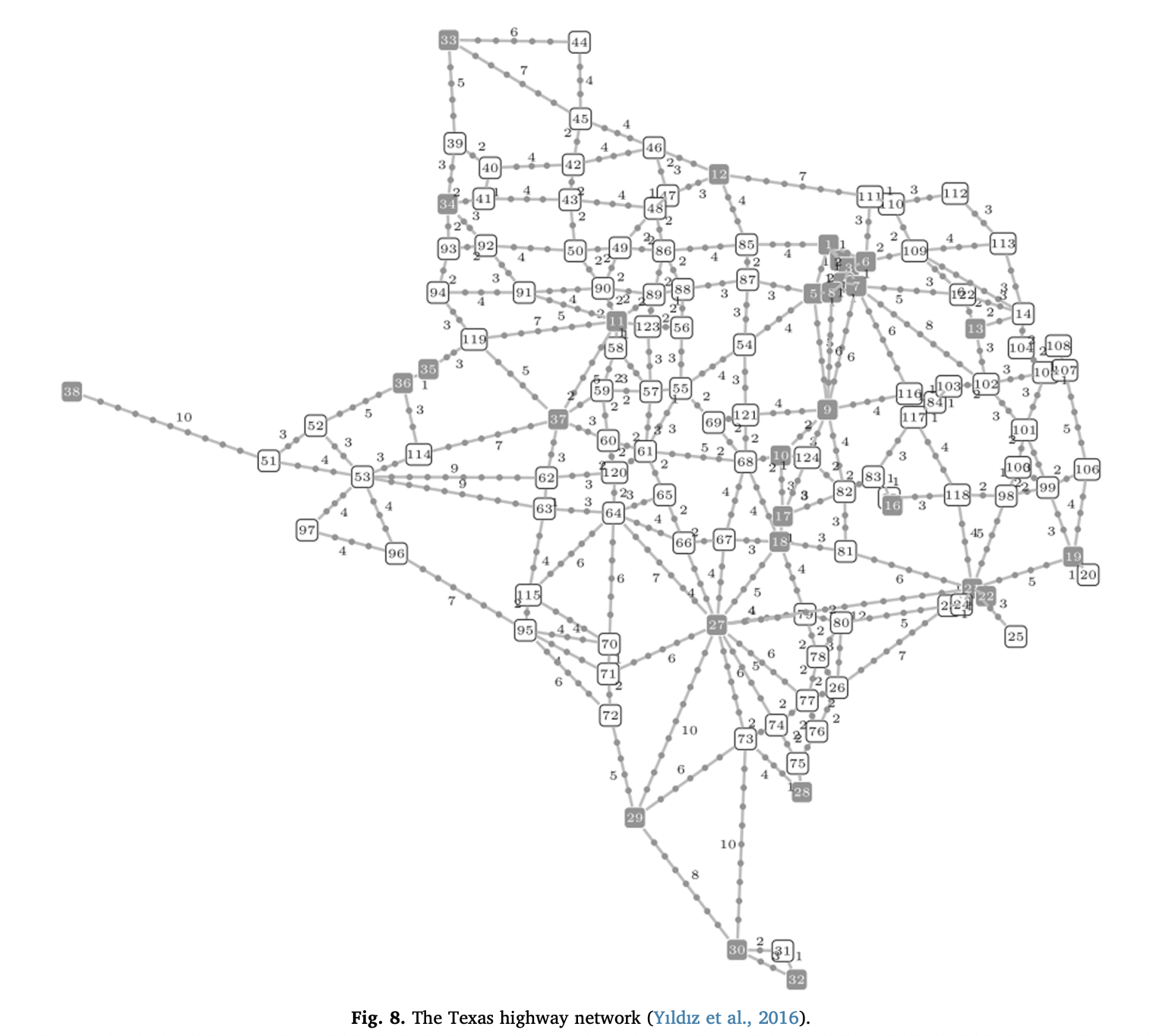
위 그림은 두번째 네트워크로, 124개의 노드와 476개의 링크가 있다. 그리고 각각의 링크에는 길이가 정해져있으며, 차량은 주행거리가 243km, 40kWh인 전기차 모델으로 선정했다. 그리고 배터리 소비량은 기존의 40kWh에서 5kWh의 편차를 갖는 유니폼분포에서 랜덤하게 정수를 뽑아냈다. 텍사스의 가장 큰 도시 30개를 출발지와 도착지로 선정했으며, 그 결과 435개의 OD-pair이 생겼다. 모든 노드를 충전소 후보지로 선정했으며, 이번 네트워크에서도 gravity model을 사용해서 flow양을 구했다.
실험에서는 다른 논문에서 그러하듯이, 출발지와 도착지에서 차량의 충전상태는 용량의 절반으로 하였으며, 운전자의 range anxiety profile은 다음 convex piece-wise polynomial function을 사용하였다.

전반적인 parameter는 다음과 같이 정하여 각각에 대해 실험을 진행했다.

알고리즘의 성능
다음은 25개 노드 네트워크에 대해서 outer-approximation algorithm의 \(\epsilon\)을 바꾸면서 실험한 결과이다.
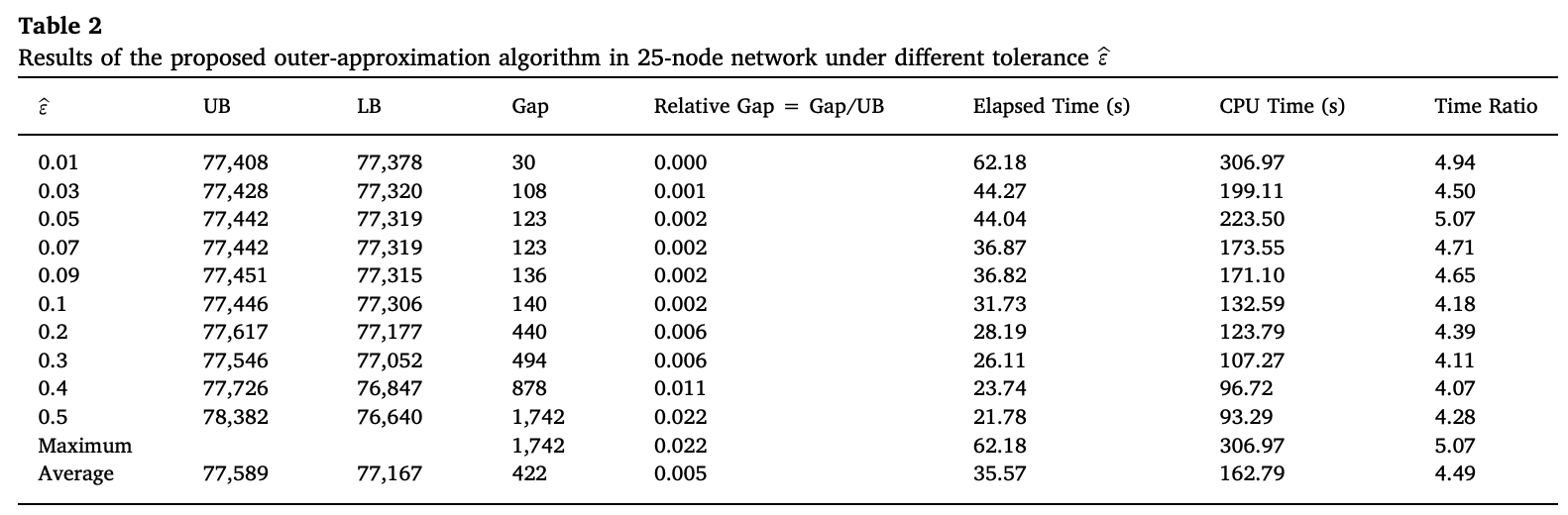
다음으로 텍사스 네트워크에 대한 실험 결과이다. 이번 실험에서는 경로 우회에 관한 오차범위를 3가지로 나눠서 실험했으며, 예산을 10단계로 나누어서 실험을 하였다.
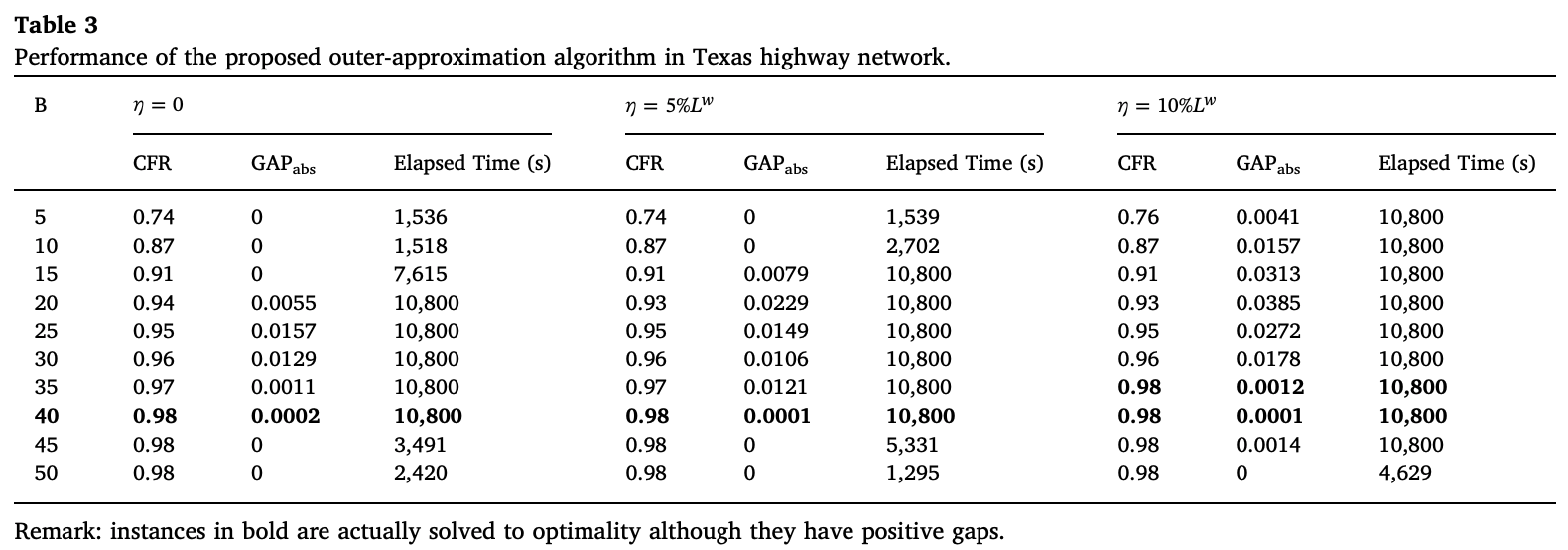
3시간 내에 풀지 못한 경우는 \(GAP_{abs}\)로 absolute optimality gap을 표기했다.
Maximum flow model과의 비교
논문에서는 EV운전자의 range anxiety를 최소화 하는 것의 장점을 보이기 위해 기존의 maximum flow model과 covered flow ratio(CFR)과 충전소의 위치를 비교하였다. 이때 최대한 최적으로 만들어주기 위해 \(\epsilon\)은 0.01으로 설정했으며 다음과 같은 결과가 나왔다.
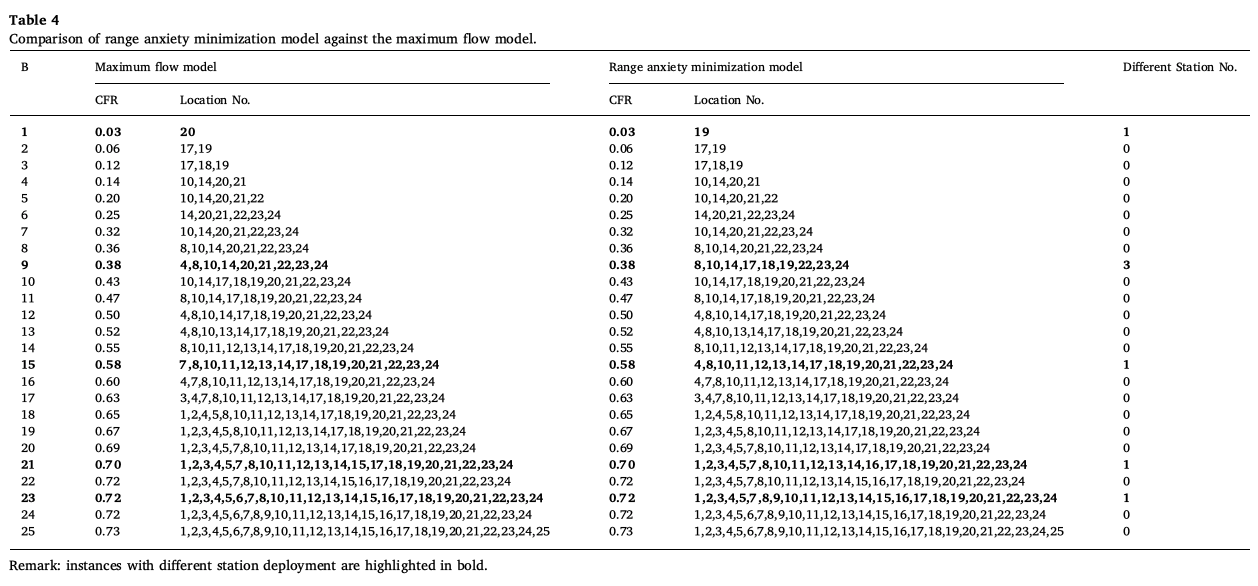
결과적으로, 거의 동일한 flow를 capture하는 것을 볼 수 있다. 논문 가장 처음 언급된 예시와 이 실험결과는 range anxiety의 효용성을 보여준다.
Extended model과의 비교
flow coverage에 charging impedance가 어떤 영향을 주는 지 실험하기 위해 DCSP와 DCSPCI를 25개 노드 네트워크에 대해 비교하였고 그 결과는 다음과 같았다.
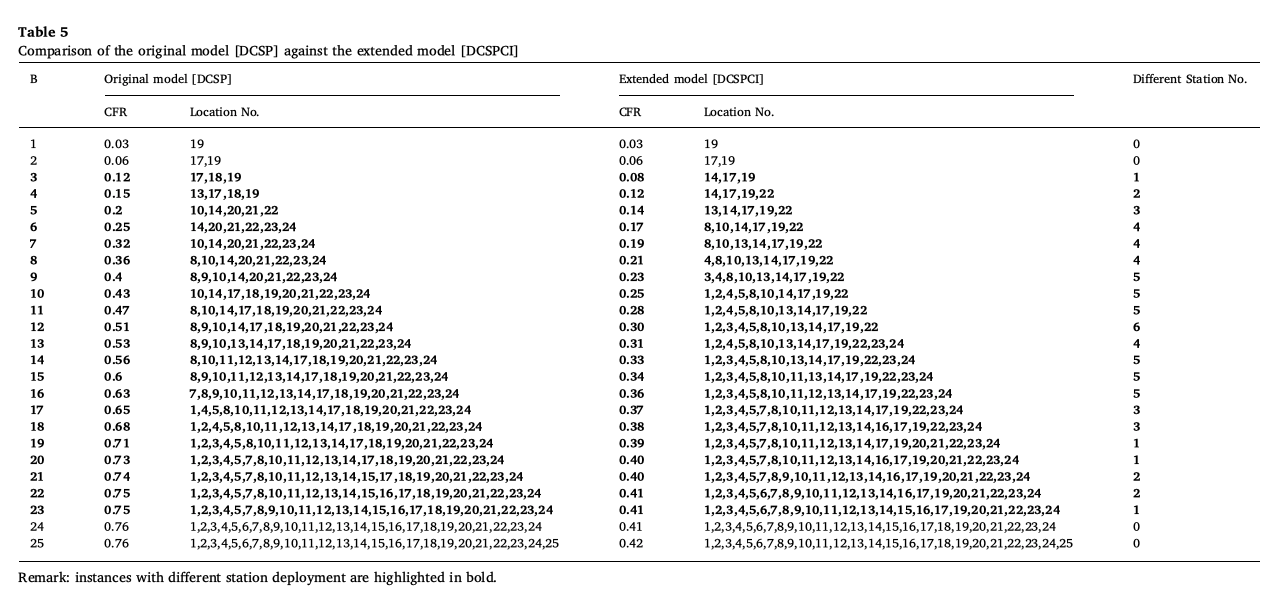
이 경우 charging impedance가 flow coverage를 상당히 줄이는 것을 볼 수 있다. 심지어 예산이 증가하면 할수록 charging impedance의 부정적인 영향이 커졌다.
Sensitivity Analysis
그리고 논문에서는 parameter에 따른 여러가지 지표들의 결과를 분석했다. 이때는 25개 네트워크를 이용해서 실험을 했다.
여기서 실험과 결과에 쓰이는 약자들을 정리하자면 다음과 같다.
- UL : Upper left corner nodes {1,2,…,9}
- MR : Middle right hand nodes {10,11,…,21}
- LB : Lower bottim nodes {22,…,25}
- CF : Covered OD pairs
- UF : Uncovered OD pairs
- CFR : Covered OD pairs ratio
- UFR : Uncovered OD pairs ratio
- ARA : Accumulated range anxiety per covered EV drivers
- MRA : Maximal driving range anxiety
먼저, 예산에 따른 결과는 다음과 같다.
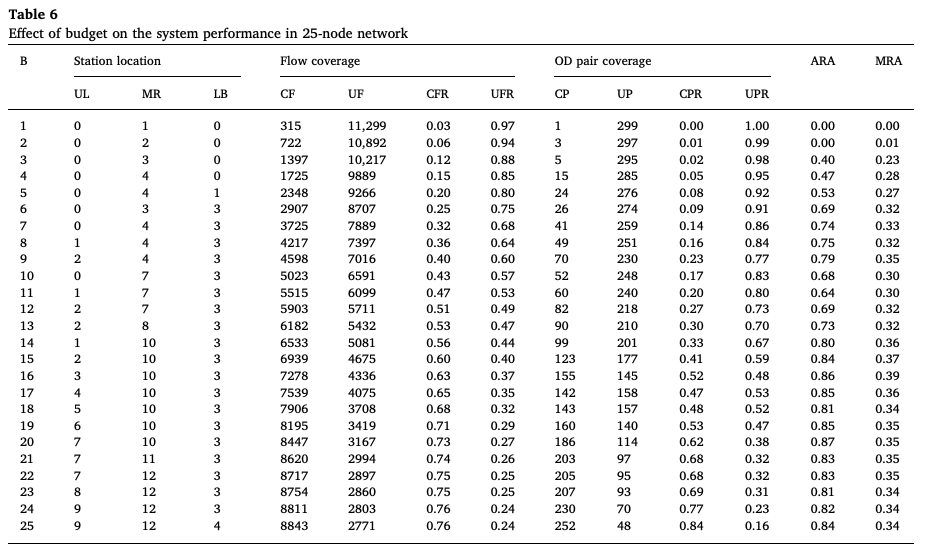
그리고 그 배터리 용량에 따른 결과는 다음과 같다.
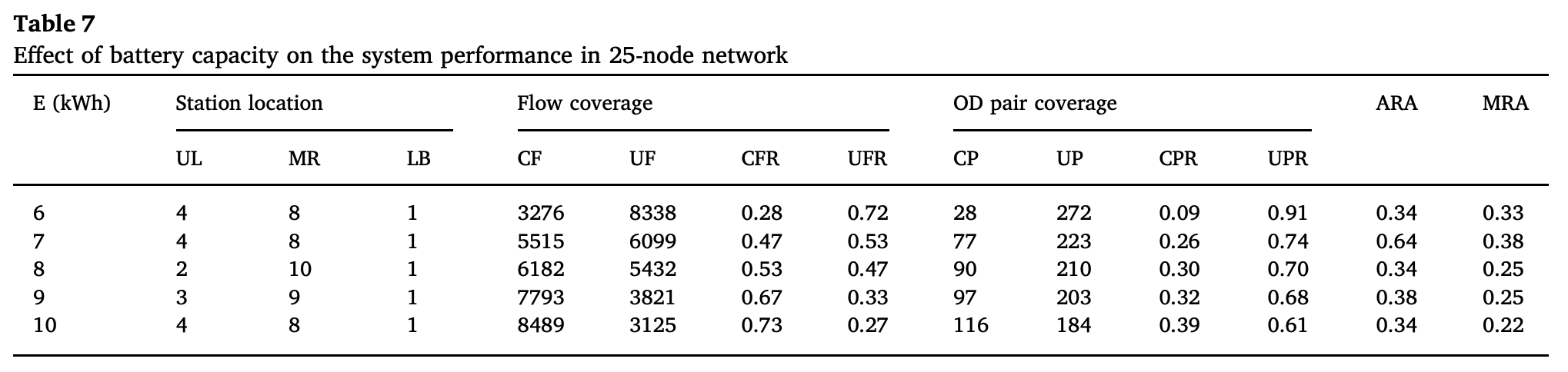
그리고 경로 우회에 대한 오차허용계수에 따른 결과는 다음과 같다.
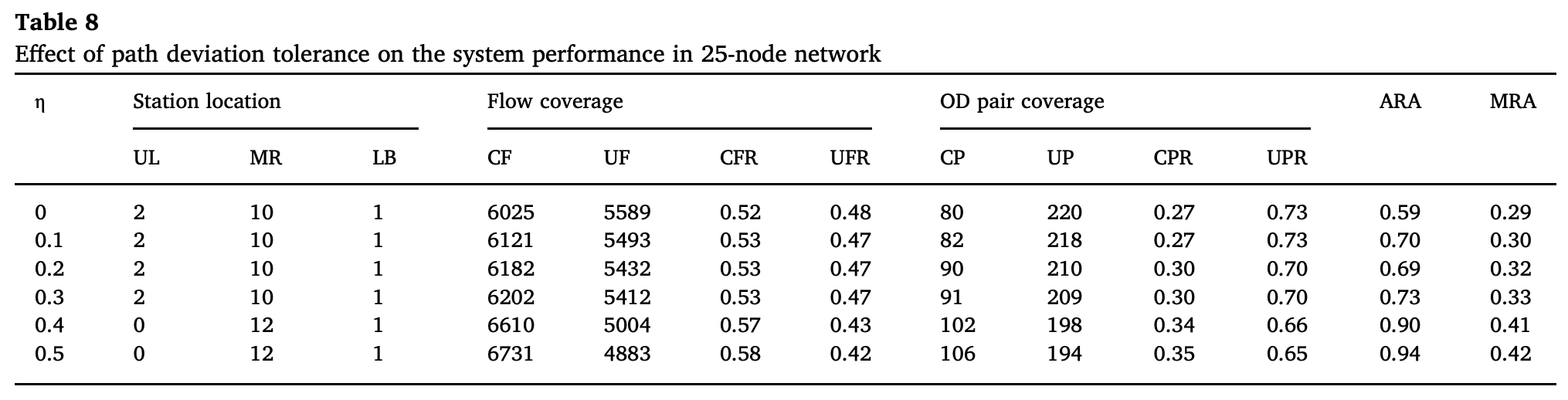
그리고 OD pair의 개수를 조절하면서 실험을 해본 결과는 다음과 같았다. 이번 경우는 텍사스 네트워크를 사용해서 실험을 했다. 원래의 OD pair 435개에서 flow의 양이 많은 OD pair순으로 내림차순으로 잘라서 OD pair의 수를 달리 하였다. 이때 FR은 Flow ratio, SNL은 same location number, SLR은 same location rate이다.
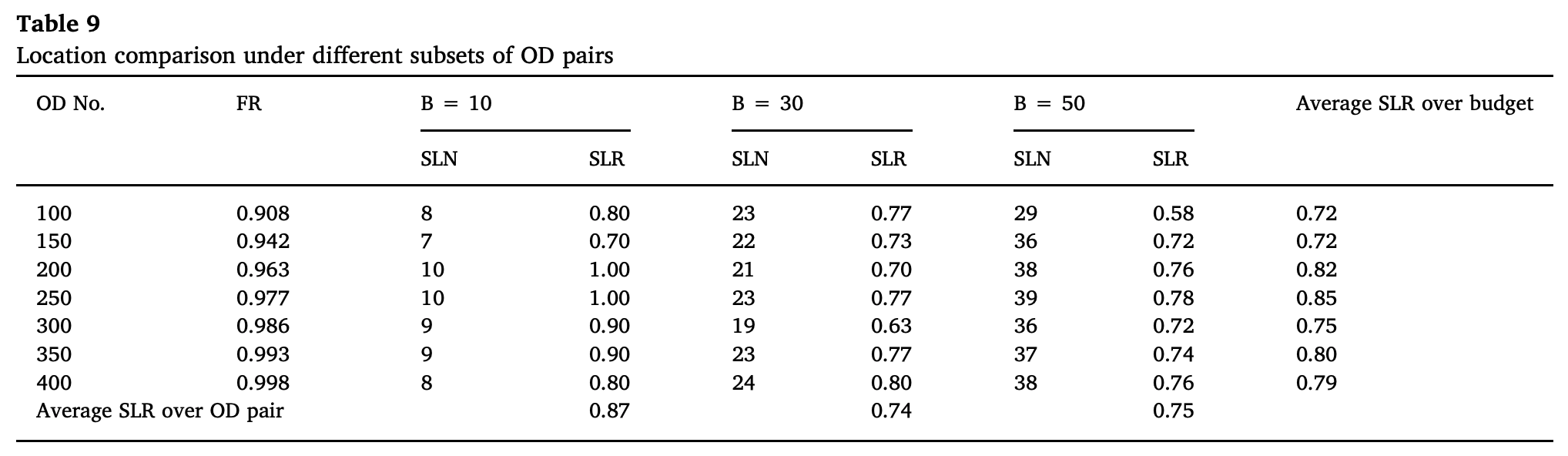
결과 및 추후 연구
-
이번 연구에서는 전기차 운전자의 불안감과 경로우회를 고려해서 전기차 충전소 입지선정 문제를 풀었다.
-
전기차 운전자들은 어떠한 기준 아래로 배터리 용량이 내려가면 불안갑을 느낀다.
-
range anxiety는 기존 연구를 따라, nonlinear한 함수로 가정되었다.
-
charging logic과 path detour behavior을 명시적으로 모델 안에 제약으로 넣어 컴팩트한 모델을 만들었고, 이를 통해 미리 경로에 대한 조합을 만들지 않아도 되었다.
-
nonlinear한 range anxiety 함수로 인해, solver로 풀 수 없었기 때문에, outer-approximation method를 사용하여 \(\epsilon\)-optimal solution을 찾아냈다.
-
charging impedance를 고려한 확장된 모델을 개발하였다.
-
25개의 노드에 대한 네트워크와 실제 텍사스 네트워크를 통해 실험을 진행하였으며, 여러가지 비교연구를 진행하였다.
-
규모가 큰 네트워크에도 효율적으로 작동하는 알고리즘이 개발될 수 있을 것이다.
-
배터리 용량에 따른 운전자의 불안감에 대한 정량적인 분석이 좀 더 필요할 것이다.
-
논문의 컴팩트한 모델이 charging demand, driving range, 전력소비량, 부분 충전, 대기열 등의 불확실성을 가진 문제와 결합한다거나 장기적인 관점에서의 계획문제와 함께 연구될 수 있을 것이다.