[논문 리뷰] Multi-period planning for electric car charging station locations: A case of Korean Expressways

이번 세미나 발표 주제는 전기차 충전소 설치 문제이다.

준비한 논문은 Multi-period planning for electric car charging station locations: A case of Korean Expressways이며,

저자는 Sung Hoon Chung, Changhyun Kwon 교수님이다.

전기차 충전소 설치 문제를 푸는 이유?

최근 환경문제로 인해 점점 전기차에 대한 수요가 늘고 있지만, 전기차 대중화에는 여전히 많은 걸림돌이 존재한다.

그리고 그 중에서도 손꼽히는 문제로는 전기자동차의 주행거리 문제, 부족한 충전소와 오래걸리는 충전 시간이다.

2014년 기준으로, 완충된 전기차는 여러가지 환경적 요소들을 고려했을 때 60~160km까지 달릴 수 있고, 이는 장거리 운전에는 부족한 주행거리다.
그렇기 때문에 장거리를 가기 위해서는 충전소를 들려야 한다. 하지만 충전소가 보통의 주유소만큼 퍼져있지 않기 때문에, 경로를 우회해서 가야하는 경우가 생기게 된다. 이러한 문제로 인해 소비자들은 전기차를 구매하기를 망설이게 되는 것이다.

현실적으로, 향후 몇년안에 전기차의 주행거리를 극적으로 올리는 것은 어렵기 때문에, 충전소를 적절한 위치에 설치하여 위 문제를 개선하고자 하는 것이다.

특히 이 논문에서는 교통량을 고려하여 여러기간에 걸친 계획(multi-period plan)을 수립하는 데에 도움을 주고자 한다.

논문에서 충전소 설치 문제를 푸는 방법

이 논문에서는 수리모형을 이용한 최적화 모델을 만들어 위치 선정 문제를 풀어낸다.

특히, flow-interceptig model을 이용한 flow-refuling location model(FRLM)에서 속도를 개선한 방법인 network expansion method를 기반으로 하여 모델링을 했다. 자세한 내용은 뒤에서 설명하도록 하겠다.

그리고 이 논문에서는 다른 논문들과는 다르게 multi-period optimal construction plan을 제시하였다.
왜냐하면, 현실적으로, 많은 충전소를 한번에 짓는 것은 한정된 예산으로는 할 수 없는 것이기 때문이다.
충전소가 많아져야 전기차가 많아지고, 전기차가 많아져야 충전소가 많아지는데(chicken-and-egg problem), 이 논문에서는 중앙정부 주도하에 충분한 시간을 갖고 충전소의 개수를 점진적으로 늘려나가야 한다는 가정하에 문제를 풀었기에 multi-period 문제를 푼 것이다.

최종적으로 이 논문에서는 다음의 세가지 방법을 제안한다.

1. multi-period optimization method
2. forward-myopic method
3. backward-myopic method

An expanded network and FRLM

앞서 언급한 network expansion과 FRLM이 무엇인지 알아보기 전에, 기본적인 가정이 존재한다.

각각의 origin-destination pair(O-D pair)에는 최단 경로가 존재하고, 운전자는 언제나 최단경로를 이용한다.

여기서 사용하는 용어를 잠깐 살펴보자면,

경로(path)란, origin에서 destination까지의 최단경로에 대한 arc들의 순서를 의미하며,

demand는 origin에서 destination까지 가기를 희망하는 차량의 수를 의미한다.

flow는 arc에 부여되는 demand의 움직임을 의미한다. 통행량 정도로 생각할 수 있다.

그리고 차량이 충전소를 거쳐서 경로를 끝까지 갈 수 있다면, 그 경로는 cover되었다고 하고, cover된 경로를 가는 차량들이 있다면 flow가 cover되었다고 한다.

network expansion technique

먼저, 논문에서는 아래와 같은 노테이션을 이용하여 개념설명을 이어나간다.

\(N^q\) : 경로\(q\)가 갖는 노드(node)의 집합 \(A^q\) : 경로\(q\)가 갖는 아크(arc)의 집합 \(G(N^q,A^q)\) : 어떤 경로 \(q\)를 갖는 노드와 아크로 이루어진 도로 네트워크 \(d_q(i,j)\) : 경로 \(q\)에 속하는 노드 \(i,j\)사이의 거리 \(ord_q(i)\) : 경로 \(q\)에서 노드 \(i\)의 순서 \(R\) : 전기차의 최대 주행 가능 거리

그리고 논문에서는 두가지 가정을 추가한다.

• 만약 경로 \(q\)위에 있는 어떤 연속되는 두 노드 \(i,j\)가 있고, \(d_q(i,j) > R\)이라면 \(i\)에서 \(j\)로 가는 것은 불가능한 것이다.
  • 따라서, 네트워크 \(G\)에는 R보다 짧은 arc만이 존재하게 된고, 만약 \(R\)보다 더 긴 arc가 있다면, arc위에 노드를 추가한다.
• origin과 destination 노드에서는 배터리의 용량이 적어도 절반은 채워져 있다.
  • 이것은 origin과 destination과 \(\frac{R}{2}\)거리 내에 적어도 하나의 충전소는 위치해야한다는 것과 같다.

이러한 가정을 통해 각 경로 \(q\)마다 source 노드, sink 노드, pseudo arc를 추가하여 expanded network를 만든다.
그리고 경로 \(q\)에 대한 expanded network를 \(G(\hat{N^q}, \hat{A^q})\)로 정의한다.

구체적으로 expanded network를 만드는 방법은 다음과 같다.

1. orgin노드 \(O\)이전에 source노드 \(s\)를 추가한다. 그리고 두 노드를 pseudo arc \((s,O)\)로 연결한다. 그리고 detination노드 \(D\)뒤에 sink노드 \(k\)를 추가하고 두 노드를 pueudo arc \((D,k)\)로 연결한다. 이는 다음과 같이 표현할 수 있다.

   

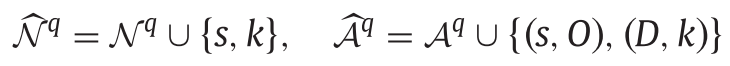
2. source 노드 \(s\)를 어떤 다른 노드와 연결한다. 만약 origin 노드에서 절반만큼 충전된 상태로 \(i\)노드로 갈 수 있다면, source노드와 경로 \(q\)에 있는 \(i\) 노드를 pseudo arc \((s,i)\)로 연결한다. 이는 다음과 같이 표현할 수 있다.

   

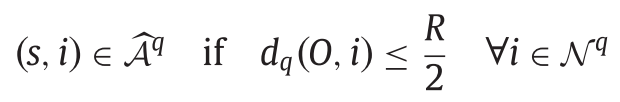
3. sink 노드 \(K\)를 어떤 다른 노드와 연결한다. 만약 경로 \(q\)에 있는 \(j\) 노드에서 절반만큼 충전된 상태로 destination 노드 \(D\)로 갈 수 있다면, 노드 \(j\)와 \(k\)를 pseudo arc \((j,k)\)로 연결한다. 이는 다음과 같이 표현할 수 있다.

   

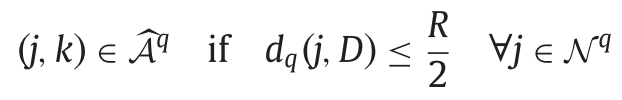
4. 경로 \(q\)위에 있는 두 노드 \(i,j\)에 대해서, 만약 \(i\)노드가 \(j\)노드보다 우선하고, 배터리가 완충된 상태로 \(i\)노드에서 \(j\)노드로 갈 수 있다면(reachable), 두 노드를 연결한다. 이는 다음과 같이 표현할 수 있다.

   

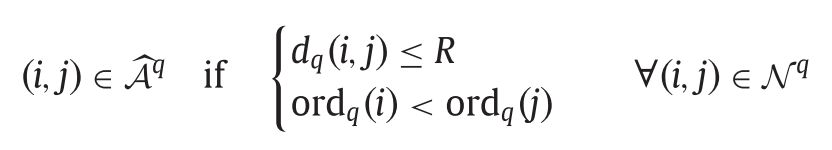
한 경로에 대해서 expanded network를 만들었다면, 가능한 모든 경로에 대해서 같은 절차를 반복해준다.

Mathematical Formulation

앞서 설명한 expanded network flow로 FRLM 수리 모형을 만들면 다음과 같다.

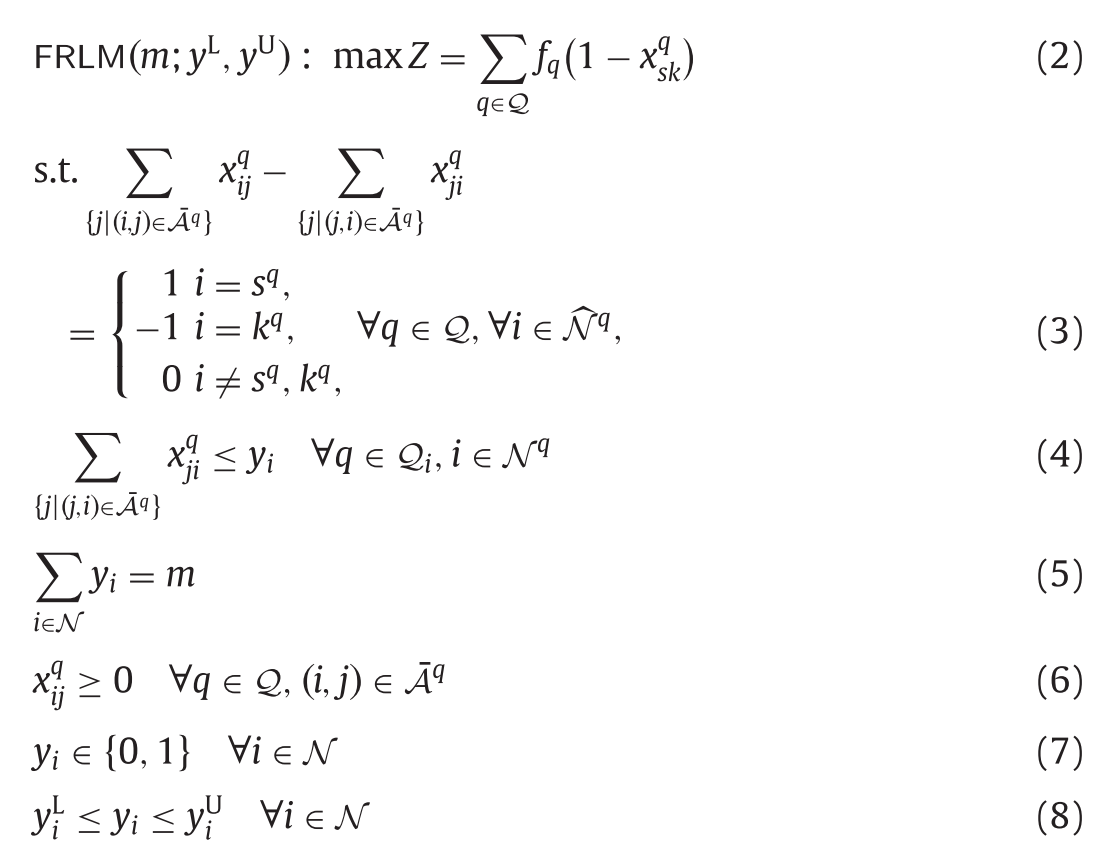
수리모형에서 목적식과 제약식의 의미는 다음과 같다.

(2) : cover된 경로들의 flow의 총합을 최대화한다.

(3) : flow balance 제약식

(4) : 충전소가 설치되지 않은 노드에서 출발하는 flow가 없다.

(5) : 충전소의 개수를 \(m\)개로 둔다.

(6) : flow는 음수가 될 수 없도록 한다.

(7) : \(y_i\)변수를 binary변수로 정의한다.

(8) : 이미 충전소가 존재하는 노드에는 \(y^L_i = y^U_i = 1\), 충전소가 설치될 수 없는 노드에는 \(y^L_i = y^U_i = 0\)으로 하고 일반적인 노드에는 \(y^L_i = 0, y^U_i = 1\)으로 두어 \(y_i\)의 값을 조절해준다.

Multi-period planning of flow-refueling locations

앞서 말했다시피, 이 논문은 초점을 multi-period plan에 맞추고 있다.

이 논문은 전기차 충전소 설치에 대한 세 가지 multi-period planning 방법을 제시한다.

1. multi-period optimization(M-opt) method

2. forward-myopic(F-myopic) method

3. bacward(B-myoptic) method

multi-period optimization(M-opt) method

M-opt방법은 M-FRLM을 기반으로 한다.

M-FRLM을 만들기 위해서는, 기간 인덱스 \(t \in \mathcal{T}, \mathcal{T} = {1,2,...,T}\)가 필요하다.

여기서 \(\mathcal{T}\)는 planning period를 뜻하며, \(T\)는 마지막 period를 뜻한다.

그리고 각 period까지 설치할 총 충전소의 개수를 뜻하기 위한 벡터 \(n\)을 다음과 같이 정의한다.

\[n = (n_1,n_2,...,n_T)^T\]

예를 들어, period 2에 설치할 충전소의 개수는 \(n_2 - n_1\)인 것이다.

그리고 \(y_i\) 대신 새로운 변수 \(y^t_i\)를 만든다.

그리고 기존의 포뮬레이션에서 목적식과 몇가지 제약식을 바꿔주어 다음과 같은 포뮬레이션을 만든다.

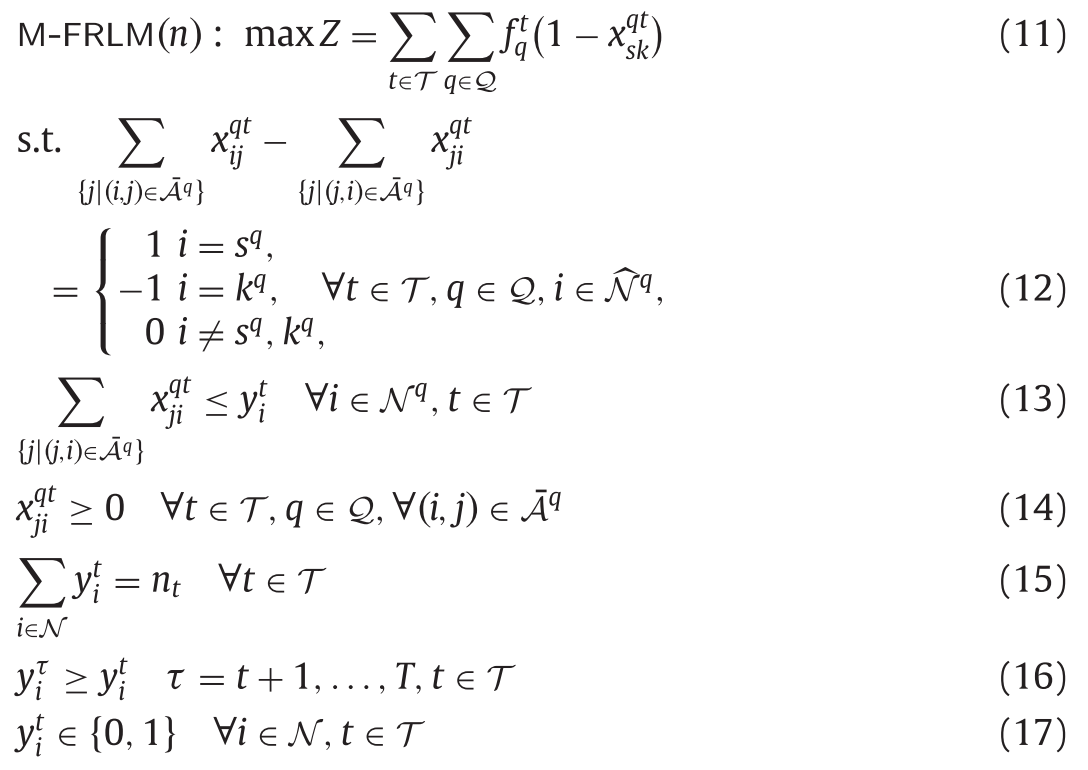
목적식에서는 time-dependent traffic volume parameter \(f^t_q\)를 추가하여 시간의 변화에 따른 통행량 변화를 고려해주었다.

(12)번 제약식에서는 기존의 flow balance 제약식에서 period를 고려해주도록 바뀌었다.

(13)번 제약식은 기간별로 달라지는 충전소 설치 지역을 고려하여 flow가 흐를 수 있도록 한다.

(14)번 제약식은 flow가 음수가 될 수 없도록 한다.

(15)번 제약식은 앞서 만든 기간별 충전소 개수에 대한 벡터를 이용하여, 기간에 따라 적절한 충전소가 지어질 수 있도록 한다.

(16)번 제약식은 한번 충전소가 지어지면 나머지 기간에 대해서도 해당 노드에는 충전소가 남아있도록 한다.

이 M-opt 방법은 M-FRLM을 branch and bound나 CPLEX와 같은 solver를 이용해서 풀기 위한 것이다.

Forward-myopic (F-myopic) method

F-myopic 방법은 첫 기간부터 차례대로 FRLM문제를 풀고, 현재 기간에서 나온 솔루션을 다음 기간에 적용하여 문제를 차례대로 푸는 것이다.

예를 들어, FRLM(\(n_1\);0,1)을 풀어 \(y^1\)이라는 답을 얻었다면 (0은 0벡터, 1은 1벡터),

이전 솔루션 \(y^1\)을 넣고 다음 기간에 대한 문제 FRLM(\(n_2\);\(y^1\),1)을 푼다.

이를 FRLM(\(n_t;y^{t-1},1\))까지 푸는 것이다.

Backward-myopic (B-myopic) method

B-myopic 방법은, 예상했다시피, F-myopic 방법의 반대다. 마지막 기간에서부터 시작한다.

예를 들어, FRLM(\(n_T\);0,1)에서 시작하여 얻은 답 \(y^T\)를 대입하여 이전 기간에 대한 문제 FRLM(\(n_{T-1}\);0,\(y^T\))를 푼다.

그렇게 첫번째 기간에 대한 문제까지 푸는 것이다.

한국 고속도로 네트워크

이 논문에서는 한국 고속도로 네트워크에 대한 실험을 진행한다. 따라서 실험결과에 앞서, 한국 고속도로 네트워크의 특징을 설명한다.

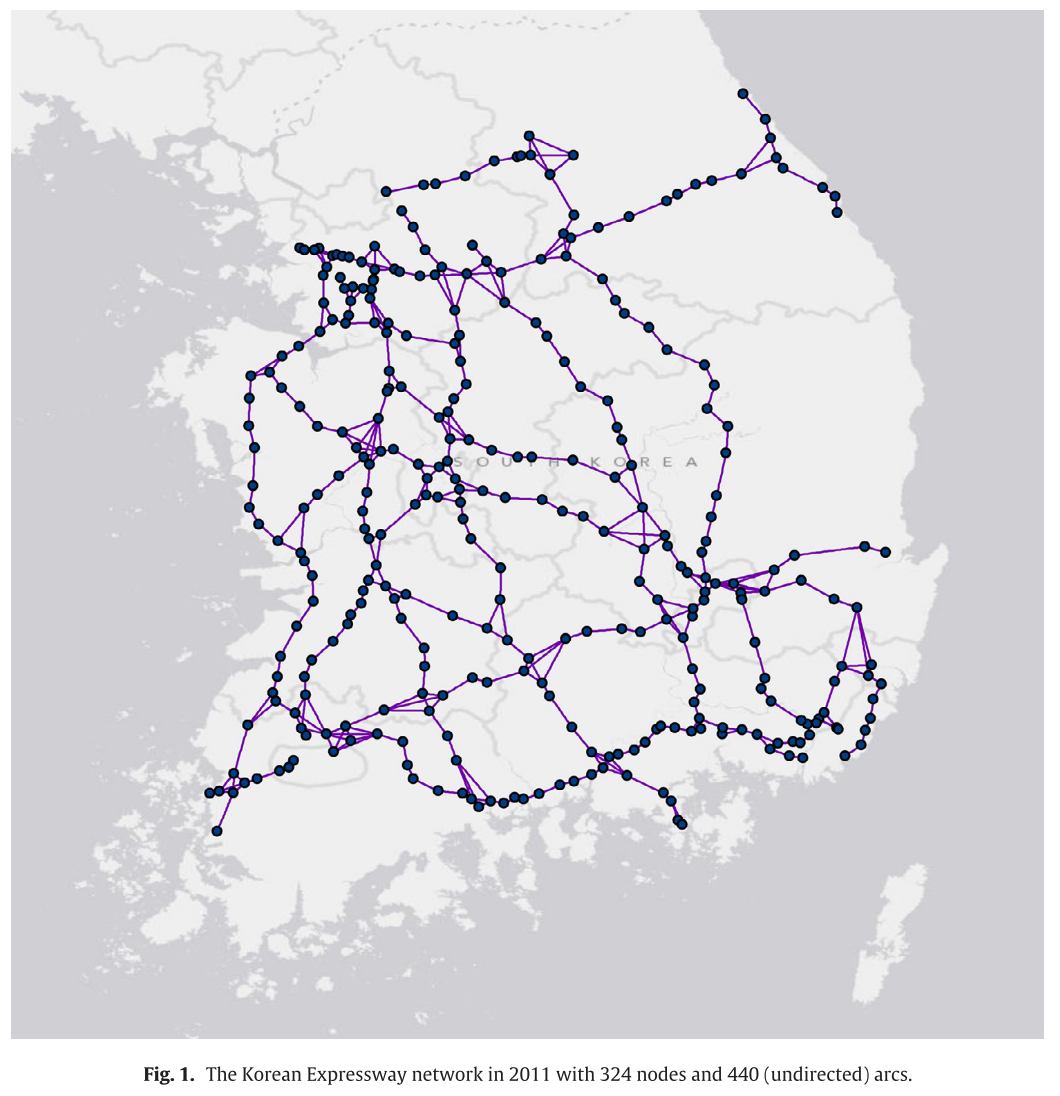
2012년 11월 기준으로 한국에는 남북으로 10개, 동서로 8개, 16개의 branch나 loop 고속도로가 있다. 대개 이러한 고속도로는 정부소유의 Korea Expressway Corporation(KEC)에 의해 유지,관리된다.

따라서 이 논문에서는 KEC에서 얻은 통행량에 대한 데이터에 근거하여 네트워크를 구성하였다.

최종적으로 324개의 노드와 440개의 undirected arc(880개의 directed arc)를 얻을 수 있었다.

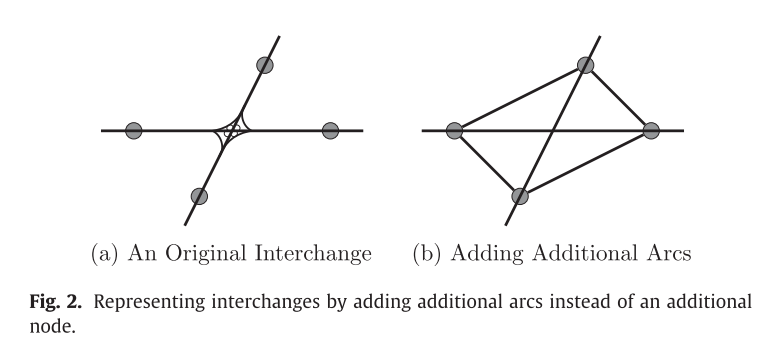
각각의 노드는 tollgate를 의미하고, 고속도로의 교차지점에서는 다음 그림과 같이 모든 가능한 경우를 고려할 수 있도록 arc를 추가하였다.

그리고 교통량 데이터는 다음과 같은 분포를 가진다.

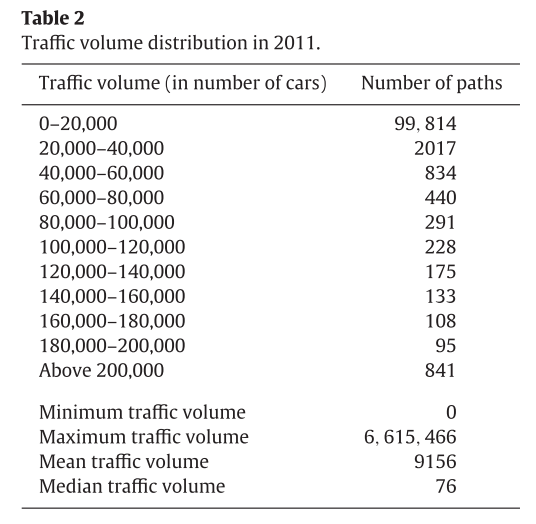
그리고 이 데이터를 통해서 모든 O-D pair에 대한 최단경로를 구했다.
그렇게 구한 최단경로의 개수는 324*323으로 104,652개였다.
경로에 대한 summary는 다음과 같다.

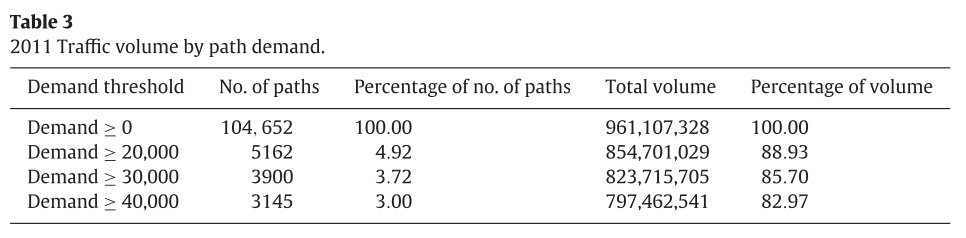
위 테이블을 보았을 때, 적은 demand를 가진 경로가 총 경로의 95%를 차지하고 있는 것을 볼 수 있다.
하지만 demand가 30000을 넘는 경우는 3900개(총 경로의 3.72%) 밖에 되지 않는 경로가 85%의 demand를 차지하고 있다.

이런 경우, 우리는 기준점을 demand가 30000이 넘는 경우를 기준으로 삼을 수 있을 것이다.

아래 그림은 각 경우에 대해 경로 길이에 따른 경로의 수의 분포를 나타낸 것이다.

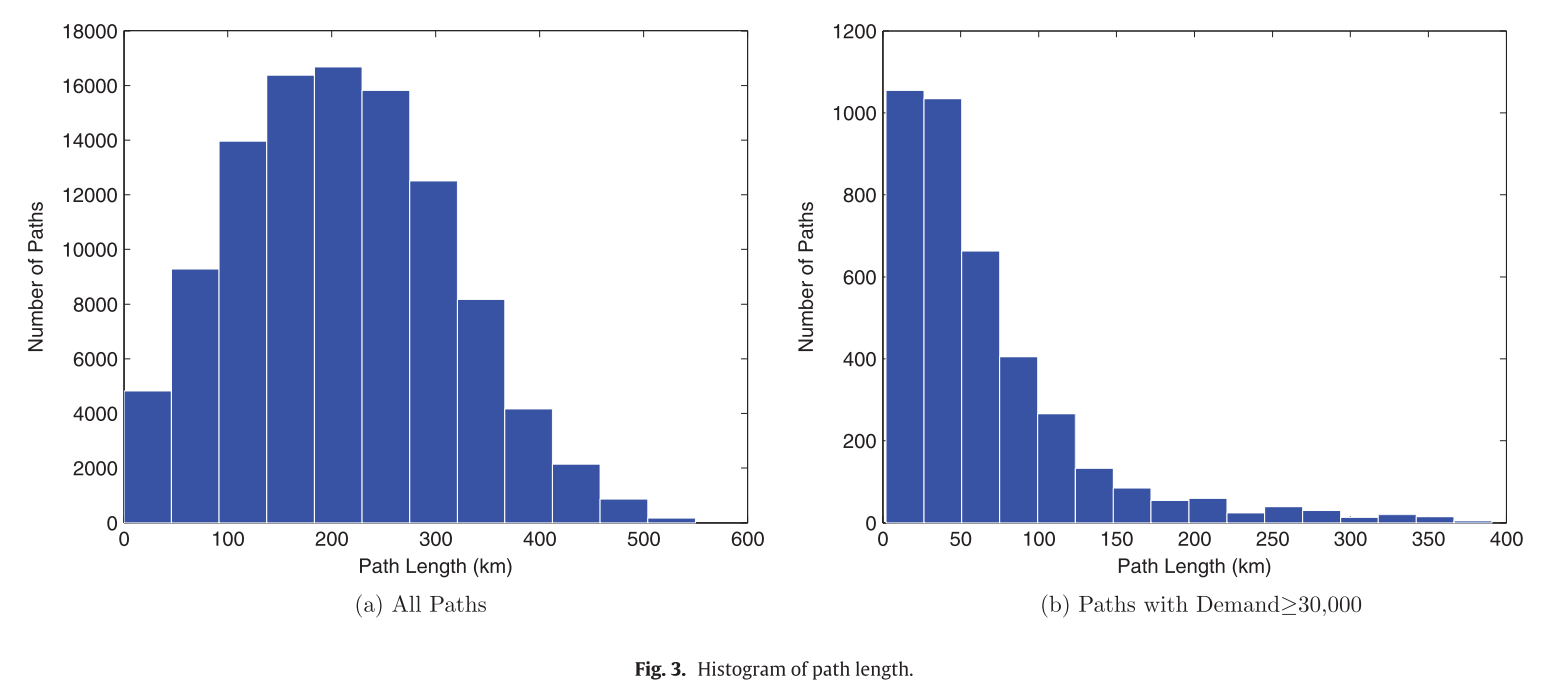
demand가 30000이 넘는 경우에는 확실히 분포가 왼쪽으로 쏠려있는 것을 볼 수 있고, 경로의 평균길이가 훨씬 더 짧아진 것을 볼 수 있다.

이와 관련해서, 다음 그림은 짧은 거리일수록 demand가 높다는 것을 보여준다.

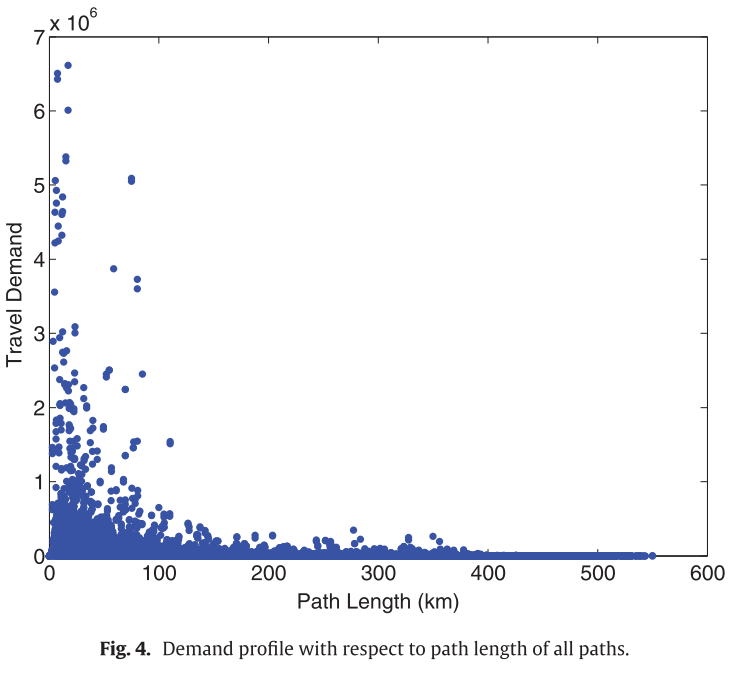
그리고 논문에서는 연구와 현실과의 차이를 언급하면서, 그 차이가 현실적용에 큰 문제가 생기지 않음을 밝히고 있다.

• 네트워크 밖에서 충전을 할 수 있지 않는가?
  • 그렇다. 하지만 한국의 고속도로 특성상, 고속도로를 나갈 때마다 이용료를 내야하고, 휴게소가 많고 편의시설이 잘 되어있다는 점에서 충전만을 위해 고속도로를 벗어날 이유는 없다고 본다.
    
    
• 논문에서 노드는 톨게이트를 의미하는데, 톨게이트에서 충전을 하는가?
  • 실제로 톨게이트는 충전을 위한 적합한 장소는 아니다. 하지만 한국 고속도로에는 충분히 많은 휴게소가 있고, 또 대부분의 휴게소가 톨게이트 근처에 존재하기 때문에 노드에 충전소를 설치한다는 것은 해당 톨게이트와 가장 가까운 휴게소에 충전소를 설치하는 것이라고 해석할 수 있을 것이다. 혹은, 휴게소에 대한 노드를 새로 만들어 모델을 바꾸는 것도 가능하다.

실험 결과

실험에서는 기간을 6개로 설정하였으며, 각 기간당 3개의 충전소를 설치하는 것으로 하였다(\(n = (3,6,7,12,15,18)^T\)).

그리고 기간에 따른 통행량의 변화는, 실험에 쓰인 2011년 데이터를 \(h_q\)를 기준으로 어떤 positive fractional constant \(r\)을 곱하여 \(f_q = rh_q\)로 설정하였다.
게다가 전기차 시장이 연간 30%씩 커질거라는 연구를 토대로, \(f^{t+1}_q = 1.3f^t_q\)로 설정하였다.

논문에서 소개된 세가지 방법으로 실험을 한 결과, 대부분의 경우 충전소가 설치된 장소는 다르게 나왔다. 다음 표는 M-opt, F-myopic, B-myopic에서 다른 솔루션의 수를 보여준다.

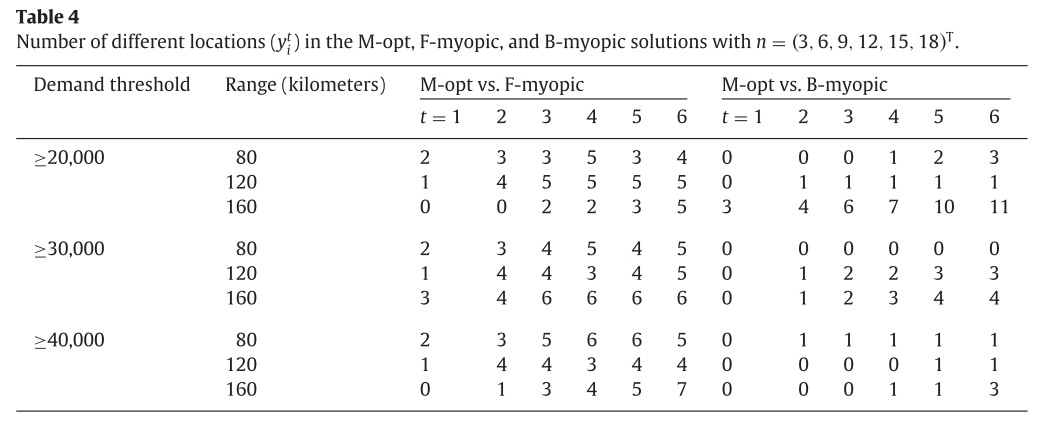
다음 그림은 demand가 20000이상이고, 주행가능거리가 120km인 경우에 대한 솔루션을 보여준다.

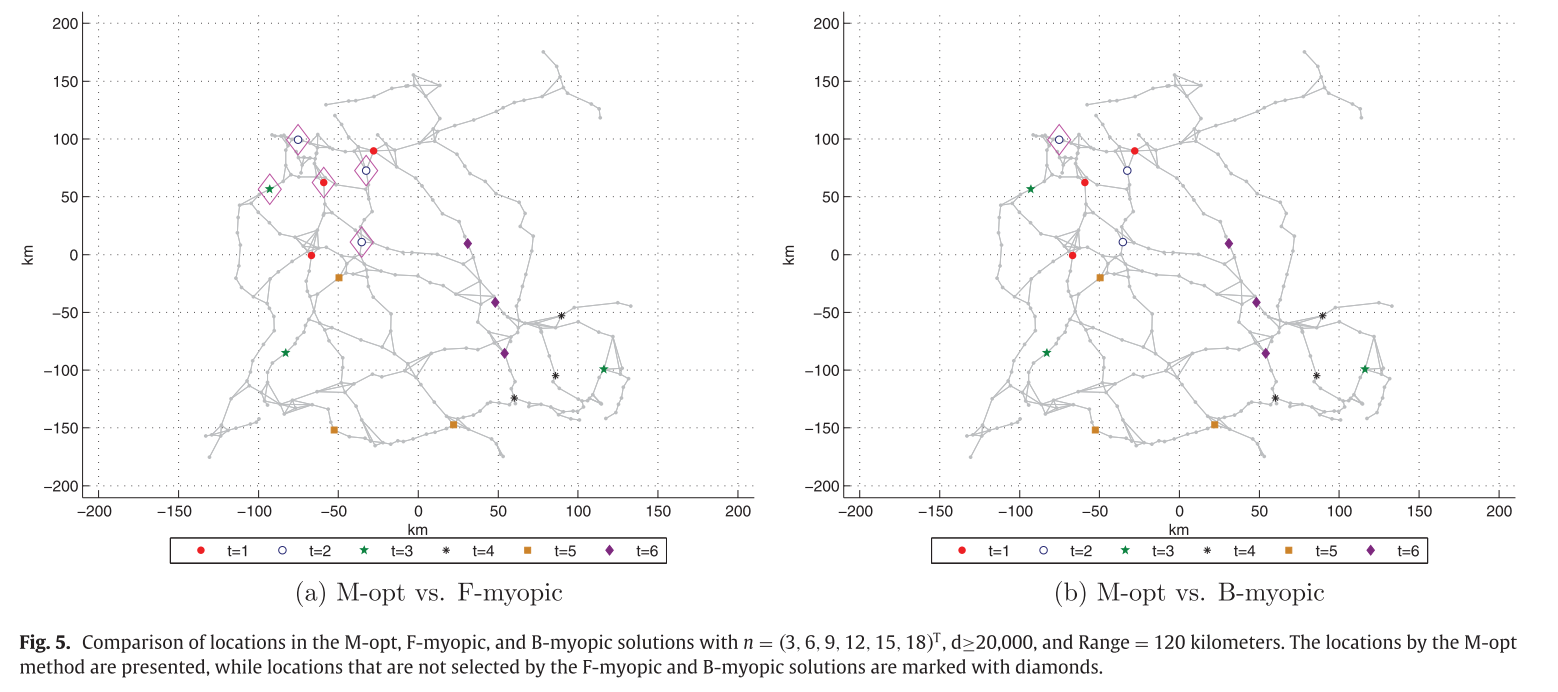
위 그림을 통해 M-opt방법과 B-myopic방법이 M-opt 방법과 F-myopic보다 더 비슷한 결과를 내는 것을 볼 수 있다.

아래 표는 각 모델별 coverage에 대한 비교결과를 보여준다. 이때 coverage는 모델에 들어간 모든 경로중에 솔루션에 의해 cover된 경로의 비율으로 정의하였다.

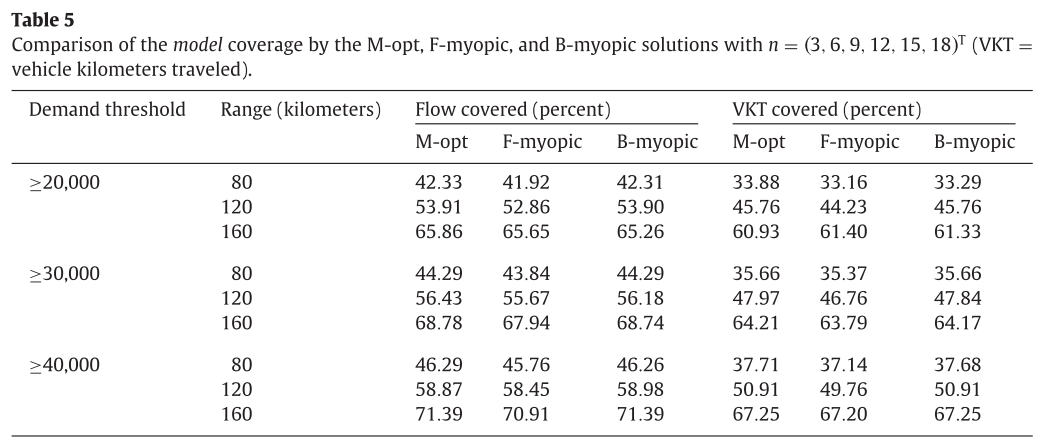
결과적으로, 한 경우를 제외한 모든 경우에 M-opt의 flow coverage가 가장 좋았고, VKT covered(Vehicle Kilomether traveled)역시 가장 좋았다. 하지만 대부분 그 차이는 1.5퍼센트 이내였다.

다음 표는 actual coverage에 대한 결과를 보여준다. 이때 actual coverage란, 모델에 들어가지 않은 모든 경로를 포함했을 때, cover된 경로의 비율을 뜻한다.

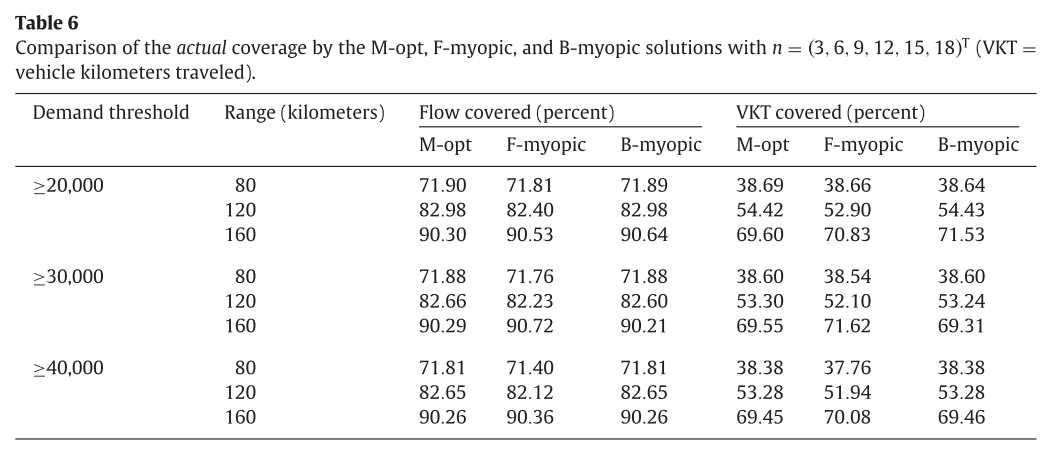
이 경우에는 다른 M-opt가 아닌 다른 모델들이 더 많은 coverage를 갖는 경우도 있었으나 그 차이는 역시 미미했다.

그리고 한국 고속도로의 경우에, 많은 travel의 길이가 짧기 때문에 결과 역시 짧은 경로를 cover하는 경우가 많이 나왔다.
다음 그림은 모델에 들어간 경로와 cover된 경로의 관계를 보여준다.

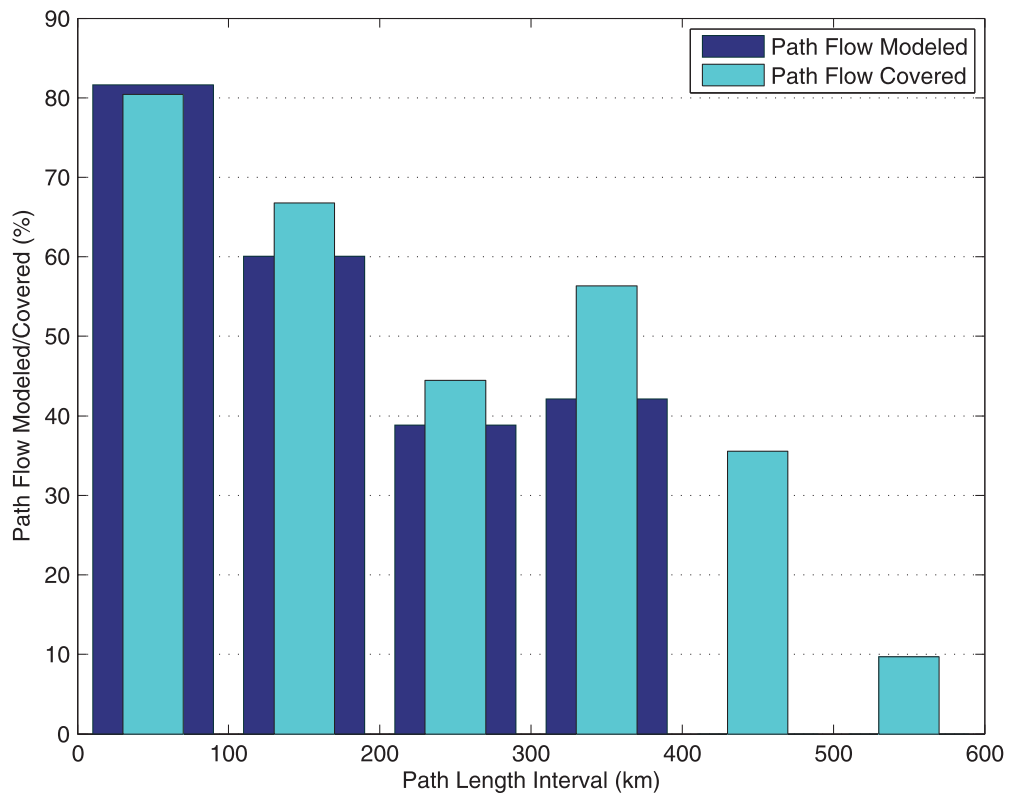
추가적으로, 400km가 넘는 경로에 대해서는 모델에 들어가지 않았지만, 그러한 경로에 대해서도 cover된 것을 볼 수 있었다.
여러개의 충전소를 거치면서 장거리 운전을 할 수 있기 때문이다.

그리고 다음 표는 세가지 모델에 대한 model coverage와 actual coverage를 보여준다.

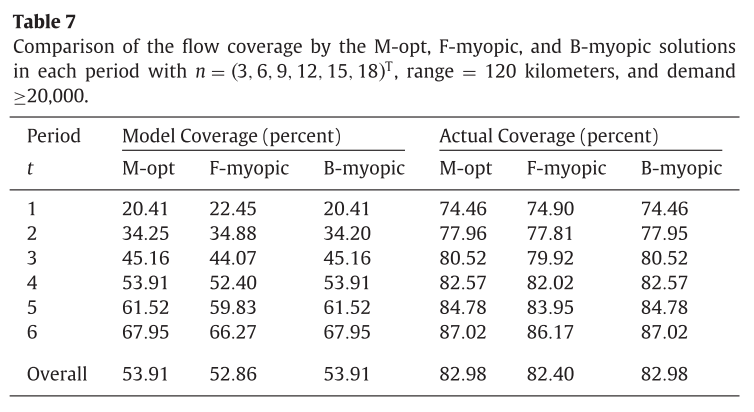
이 경우, M-opt와 B-myopic은 똑같은 결과를 보여주었고, F-myopic은 초반 기간에 집중되어 후반기간에서 상대적으로 좋지 못한 결과를 만들어냈다.

세가지 방법의 솔루션은 비슷했지만, 실험 속도면에서는 B-myopic 방법이 좋았다. 관련 결과는 다음 표를 통해 알 수 있다.

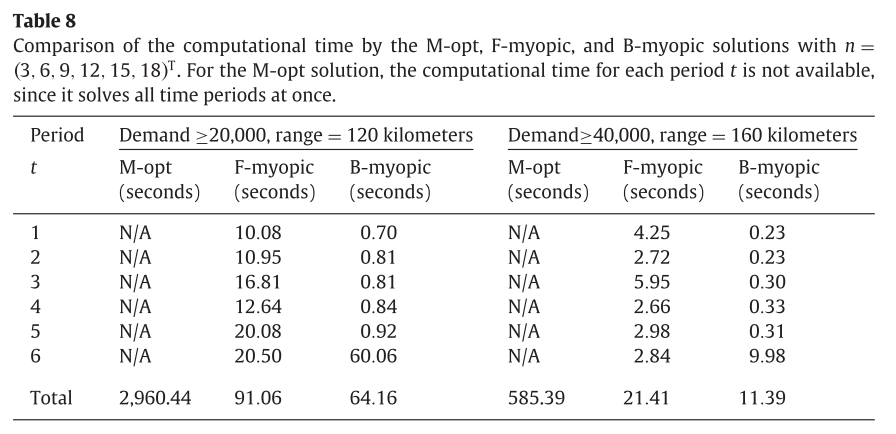
M-opt의 경우에는 기간별로 문제를 푸는 것이 아니기에 데이터가 존재하지 않는다. 하지만 총 시간은 다른 두 방법에 비해 상당히 오랜 시간이 걸린 것을 볼 수 있다. 기간이 늘어날수록 decision variable이 빠르게 많아지기 때문이다.
F-myopic방법의 경우에는 각 기간별로 비슷한 시간이 걸렸지만, B-myopic 방법은 처음(가장 마지막 기간)에는 시간이 오래 걸리나 이후에는 굉장히 빠르게 문제를 풀어 세가지 방법중에 가장 효율적인 것으로 나타났다.

추가적인 실험과 통찰

앞서 실험에서 세개의 방법에 큰 차이가 없었기 때문에 논문에서는 5개의 다른 demand profile을 가지고 추가적인 실험을 한다.

5개의 demand profile은 다음과 같다.

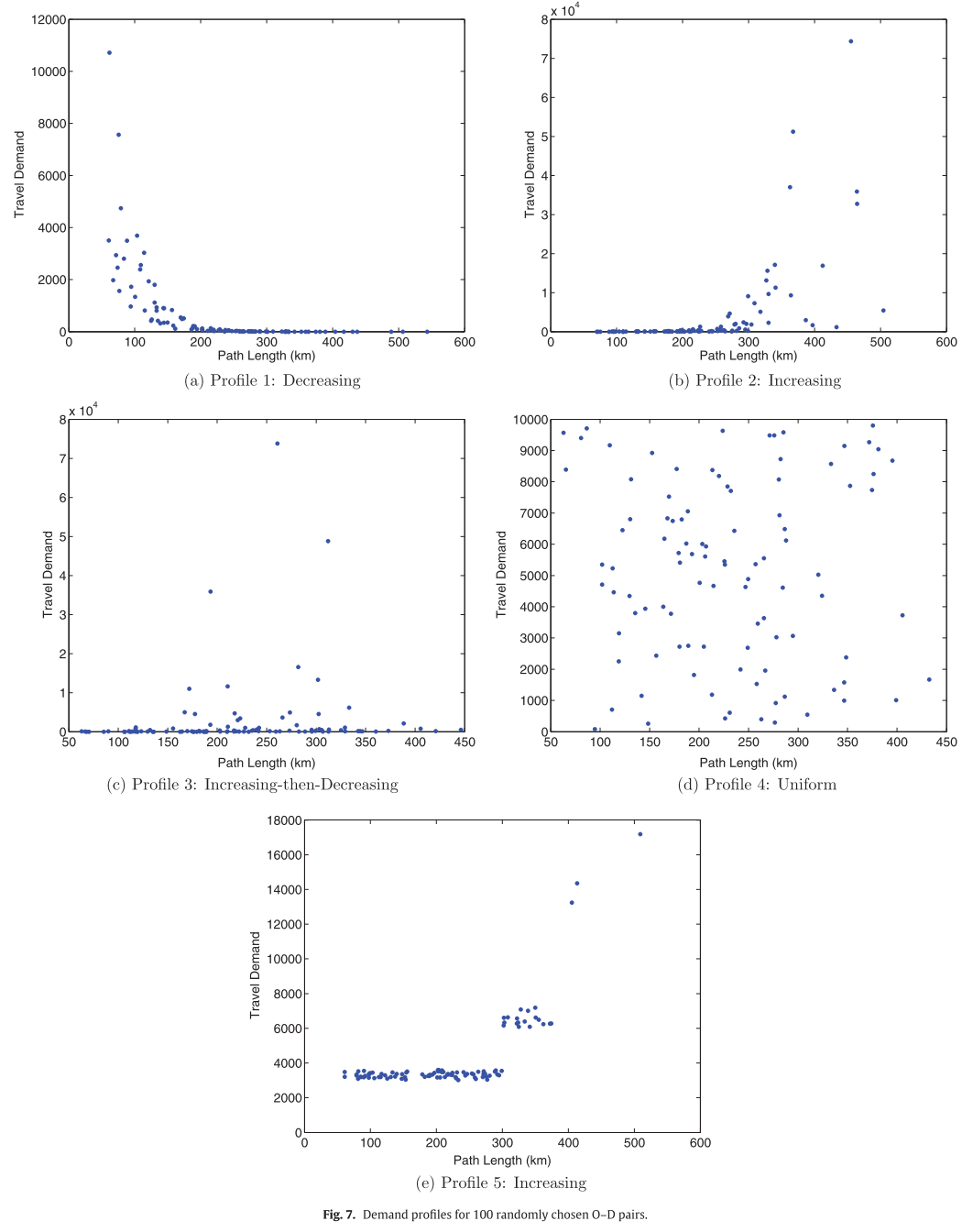
각 demand profile은 한국 고속도로 경로에서 무작위로 선택된 100개의 O-D pair로, profile 1은 원래의 demand 양상과 비슷하고, profile 2는 길이가 긴 경로일수록 demand가 높아지도록 하였다. profile3는 중간길이의 경우에 demand가 많고, profile4는 일정한 demand를 갖도록 하였다. profile5에서는 계단식으로 demand가 높아지도록 하였다.

기간은 3개로 나누었으며, \(R = 120\)으로 하였다. 다른 조건은 이전 실험과 동일하게 설정하였다.

그 결과는 다음 표에서 확인할 수 있다.

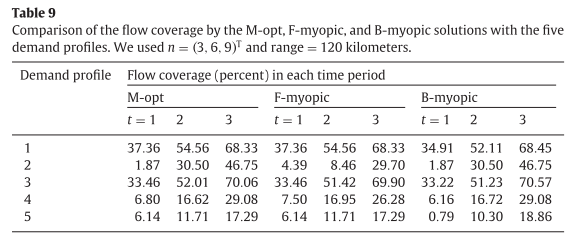
profile1의 경우는 기존의 실험결과와 유사했다. 하지만 profile2에서 F-myopic방법이 후반 기간에서 coverage가 상대적으로 매우 좋지 않은 것을 볼 수 있었다. 긴 경로를 cover하기 위해서는 M-opt나 B-myopic방법이 효율적인 것으로 보인다. profil3,4의 경우에는 초기에는 M-opt와 F-myopic방법이 유사하며 B-myopic보다 coverage가 좋지만 후반으로 갈 수록 B-myopic의 coverage가 좋아져 B-myopic이 마지막 기간에는 coverage가 좋은 모습을 보여준다. 하지만 전체적인 coverage는 역시 M-opt가 좋은 것을 볼 수 있다. profile5에서는 B-myopic방법이 마지막 기간에는 가장 좋았으나, 전체적인 coverage는 다른 두 방법에 비해 낮았다. 첫번째 기간에 다른 방법들은 6.14를 cover한데 반해 0.79만을 cover한 것이 그 이유이다. 이런 경우 B-myopic방법은 chicken-and-egg문제를 제대로 풀기 어려울 수 있다.

결론과 추후연구

• 한국 고속도로에 대한 현실 데이터를 기반으로 전기자동차 충전소에 대한 multi-period 입지선정 문제를 풀었다.

• 계산속도를 위해 차량의 주행거리에 절반보다 짧은 경로를 배제하였으며, 일정 기준점보다 demand가 적은 경로에 대해서도 배제를 하였다.

• M-opt method, F-myopic method, B-myopic method를 제안했으며, 한국 고속도로 데이터에 대한 실험결과는 세 방법에 큰 차이가 없었다.

• 다른 데이터를 통해 추가적인 실험을 해본 결과, F-myopic과 B-myopic은 어떠한 경우에 좋지 않은 결과를 만들었다.

• M-opt method는 모든 경우에 가장 좋은 답을 얻을 수 있지만, 시간이 오래걸린다는 단점이 있다. 그리고 기간이 많아질수록, 문제의 사이즈가 급격히 커지지만, F-myopic이나 B-myopic은 상대적으로 천천히 증가한다.

• 따라서 문제 사이즈가 큰 경우에는 B-myopic 방법을 사용하는 것이 좋아보인다. 하지만 demand 분포를 잘 고려해야 한다.

• 추후 연구로, capacity에 대한 고려를 할 수 있을 것이다.

• stochastic한 충전시간을 고려하는 것과, 각 충전소마다의 demand와 대기 시간등을 고려하는 것 또한 가치가 있을 것이다.

• 그리고 시간이 지날수록 전기차의 이동거리가 늘어날 것으로 전망되기에, 그러한 부분도 고려하면 좋을 것이다.

참고

• Multi-period planning for eletric car charging station locations: A case of Korean Expressways