이번 연구실 세미나에서 발표할 논문은 “The hub covering flow problem”이다.
Hub covering flow problem(HCFP)이란?
HCFP는 hub-and-spoke(대도시 거점 노선 운항 방식)네트워크에서 non-hub node들을 hub-node에 할당하면서 최소한의 비용으로 hub node를 배치하는 문제이다.
여기서 hub-and-spoke란 다음 그림과 같이 hub노드들을 중심으로 여러 노드가 연결되어 있는 방식의 네트워크이다.

이러한 hub-and-spoke방식은 일상 생활에서도 많이 찾아볼 수 있다. 예를 들어, 항공망, 우편망, 통신망, 공공교통체계, 운송망 등이 hub-and-spoke방식을 사용한다.
일반적으로 이러한 hub location problem에서는 노드들의 부분집합이 hub로 선택된다. hub 노드는 다른 노드들을 서로 연결하는 역할을 하고, non-hub 노드들은 single assignment나 multiple-assignment규칙에 의해 hub노드들에 연결된다.
single assignment network : 각 노드들이 정확히 하나의 hub 노드에 연결된다.
multiple assignment network : 각 노드들이 적어도 하나의 hub 노드에 연결된다.
이 논문에서는 single assignment network만을 다루고 있다.
그리고 hub-and-spoke 시스템에서 demend는 origin node에서 destination node까지의 flow로 표현이 된다.
hub location problem에는 다양한 변종 문제들이 존재한다.
\(p\)-hub median problem, the hub covering problem(HCP), the \(p\)-hub centre problem, hub arc location problem …
이 논문에서는 uncapacitated hub location problem(UHLP)와 the hub covering problem(HCP)의 특징들을 결합한다.
Uncapacitated hub loaction problem(UHLP) : hub를 여는 총 비용과 demand flow에 대한 운송비용의 총합을 최소화하는 네트워크를 찾는 것인데, demand flow에 어떤 capacity제약도 존재하지 않는 것이다.
하지만 어떤 경우에는 노드간의 거리에 관한 제약이 필요할 수도 있다. 예를 들어, 항공네트워크에서는 비행기의 최대비행거리를 고려해줘야 할 것이다.
이러한 제약은 location theory에서의 제약과 비슷하다. 설비와 demand point와의 거리가 설비의 커버반경 안에 들어온다면 cover되었다고 할 수 있고, 이러한 set covering problem은 설비의 설치 비용을 최소화하는 설비위치를 찾을 수 있다.
HCP에서 set covering problem의 개념을 처음 도입하고자 했던 Campbell은 coverage에 대한 서로 다른 세가지 정의를 제안했다.
An origin-destination pair (\(i\),\(j\)) is covered if
- the total length of the path from node \(i\) to node \(j\) through hub k first then hub \(l\) does not exceed a specified value
- the length of each link in the path from node \(i\) to \(j\) through hub k first then \(l\) does not exceed a specified value
- the length of each of the links connecting a non-hub node to a hub node in the path from node \(i\) to \(j\) does not exceed a specified value
이 논문에서는 세번째 정의를 coverage의 정의로 사용했다.
이 논문에서는 hub covering flow problem(HCFP)를 통해 coverage를 충족시키면서 설비비용과 demand flow운송 비용을 최소화하는 방법을 제안한다.
Model Formulation (HCFP)
이 논문에서는 single-assignment network를 사용해서 문제를 풀었으며, UHLP에서의 multi-commodity flow formation을 기반으로 formulation을 만들었다.

- \(N\): 네트워크의 노드의 집합
- \(Z_{ik}, \forall i,k \in N\): node \(i\)가 hub \(k\)에 할당되면 1, 아니면 0인 binary variable
- \(Z_{kk} = 1\)이라면, node \(k\)가 hub노드인 것이다.
- \(F_k, \forall k \in N\): node \(k\)에 대해 설치,운영비를 연간으로 환산한 비용
- \(W_{ij}\): node \(i\)에서 node\(j\)까지의 demand flow
- \(O_i\): node \(i\)에서 시작한 총 demand
- \(D_i\): node \(i\)로 끝나는 총 demand
- \(c_{ij}\): node \(i\)에서 node \(j\)로 한 unit이 이동하는 비용
- \(\alpha\): transfer cost factor
- \(\chi\): collection cost factor
- \(\delta\): distrubution cost factor
- \(\alpha\), \(\chi\), \(\delta\)는 운송비용 \(c_{ij}\)를 스케일링하는 데 사용된다. 그리고 \(c_{ij}\)는 symmetric하다고 가정했다.
- \(Y^i_{kl}\): 노드 \(i\)에서 시작하여, hub \(k\)를 지나고 hub \(l\)을 지나는 flow의 양
- \(A_{ik}, \forall i,k \in N\): non-hub node \(i\)가 node \(k\)에 있는 hub에 cover되었다면 1, 아니면 0인 binary variable
- 이 matrix를 통해 모델의 사이즈를 줄일 수 있다. 아래 (2)번 제약에서 볼 수 있다.
목적식
hub의 총 연간비용, hub간의 demand 운송비용, non-hub와 hub 사이의 운송비용을 각각 더한 것을 minimize하는 것이다.
제약식
(2) : node \(i\)를 cover할 수 있는 node \(k\)에만 node \(i\)가 할당될 수 있도록 한다.
(3),(7) : 네트워크가 single assignment rule을 따르도록 한다.
(4) : 각 노드 \(i\)와 hub에 대한 flow conservation 제약이다.
(5) : hub network에 존재하는 link들을 통해서만 flow가 흐를 수 있게 해준다.
실험 결과
-
잘 알려진 데이터셋인 Civil Aeronautics Board(CAB)으로 실험을 했다.
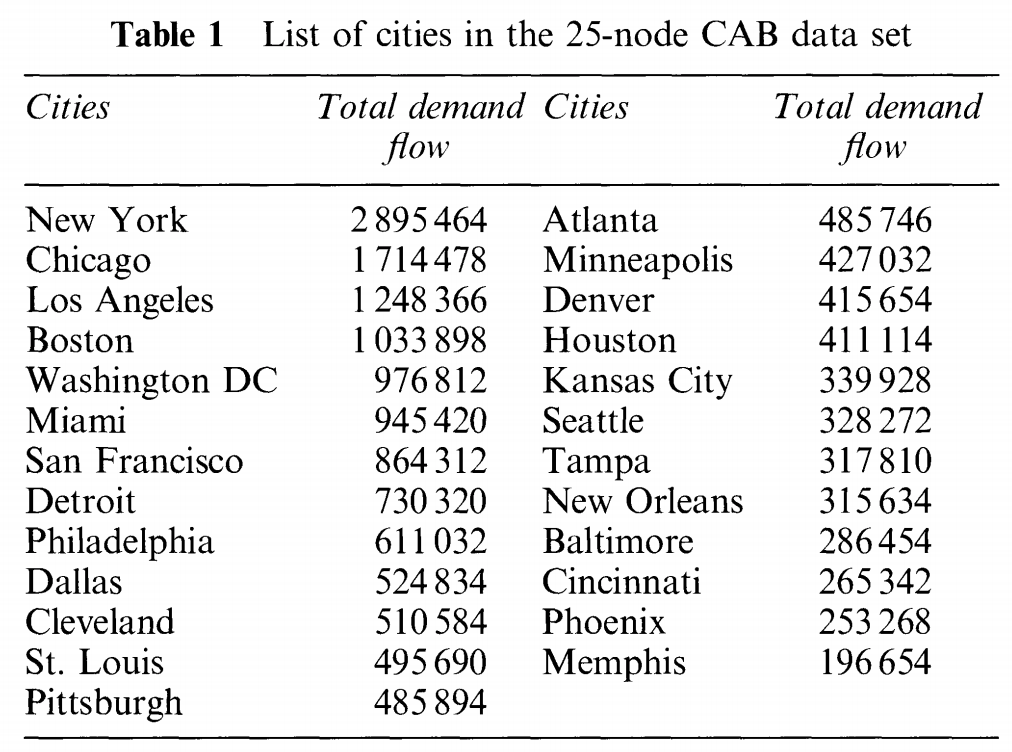
-
CAB 데이터셋에는 고정비에 대한 내용이 없기 때문에, 논문에서는 두가지 방법을 사용하여 고정비를 만들었다.
- constF : hub가 어디에 위치하든, 같은 비용으로 open된다고 가정한다.
- \[F_k = F, \forall k \in N\]
- 이 경우, \(F\)는 5000에서 50000사이의 값에서 5000씩 값을 증가시키면서 실험을 했다.
- diffF: : 각 노드별 총 demand flow에 따라 hub의 고정비를 다르게 한다.
- \[F_k = \frac{O_k+D_k}{\theta}\]
- 위 식에 따르면, demand flow가 클 수록 hub를 open하는 비용이 높아진다.
- scaling parameter \(\theta\)를 통해 opening비용과 운송비용간의 비율을 조정할 수 있다.
- 논문에서는 \(\theta\)를 10,20,30,40,50으로 두고 실험을 했다.
- constF : hub가 어디에 위치하든, 같은 비용으로 open된다고 가정한다.
- 실험에서 각 hub에 대한 coverage radius는 네트워크에서 가장 긴 link와의 비율에 따라 설정하였다.
- \(\Delta\)를 네트워크에서 가장 긴 link의 길이라 했을 때, 0.1\(\Delta\), 0.2\(\Delta\), …, 0.5\(\Delta\)를 실험에 사용하였다.
-
\(c_{ij}\)는 \(\frac{d_{ij}}{25000}\)으로 설정하였다. 이때, \(d_{ij}\)는 노드 \(i\)와 \(j\)의 최단 경로 거리이다.
-
\(\alpha = 0.75, \chi = 1, \delta = 1\)으로 설정하였다.
-
CPLEX 12.3, Intel Core 2 2.13GHz, 2RAM으로 실험을 진행했다.
-
constF에 대한 실험결과는 다음과 같다.
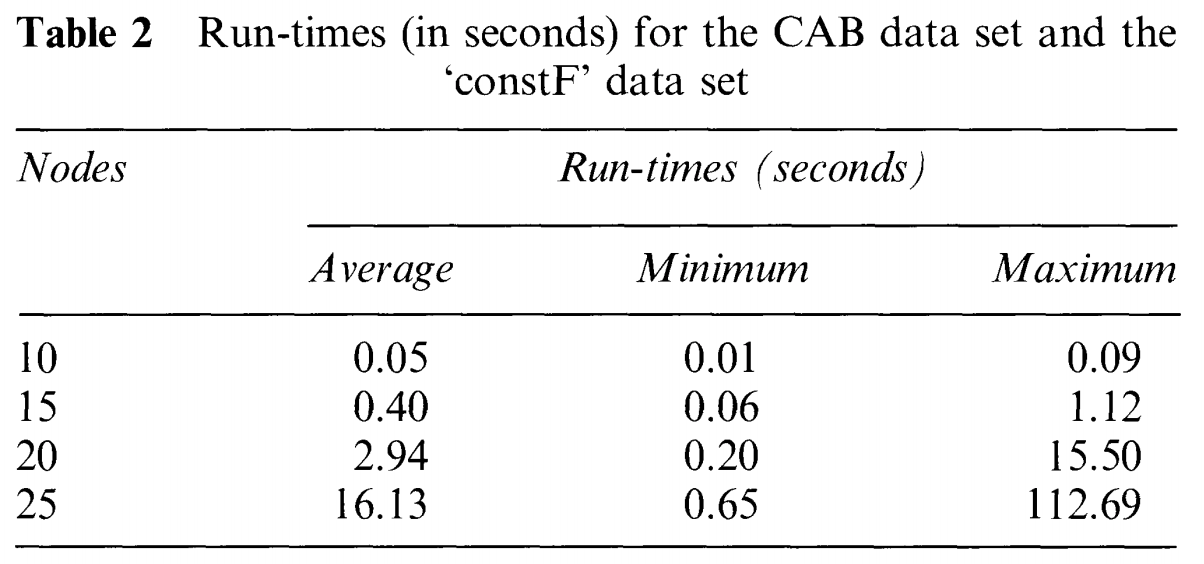
-
diffF에 대한 실험결과는 다음과 같다.
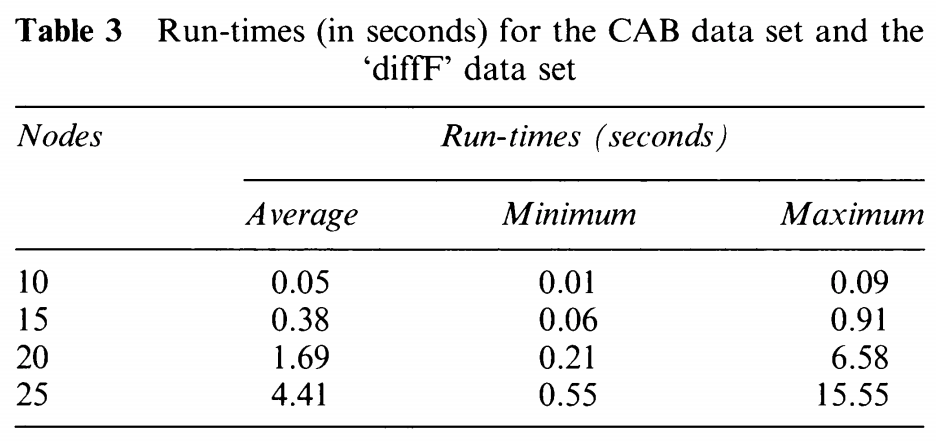
-
다음 그래프는 constF에서 고정비와 coverage radius에 따른 hub의 개수변화를 나타낸다.
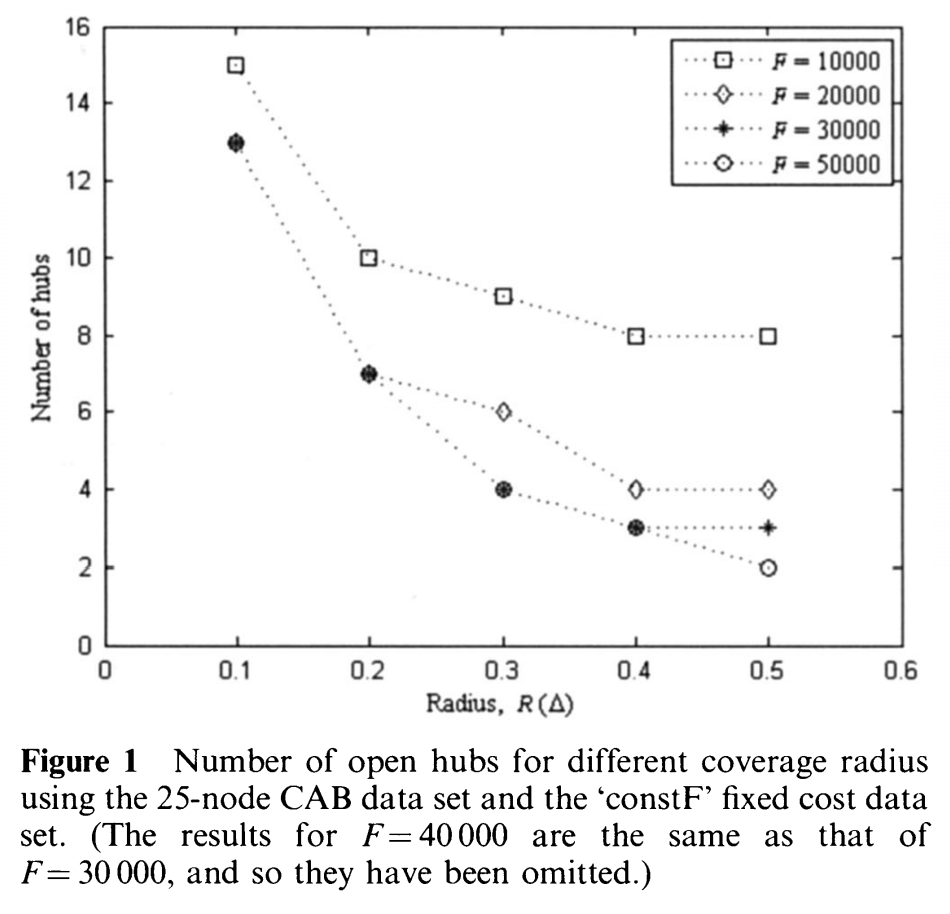
-
하나의 그래프는 같은 고정비에 대해서 radius의 변화를 나타낸다.
-
당연히, 고정비가 증가하면 hub의 개수가 줄어드는 것을 볼 수 있다.
-
cover 반경이 커지면 hub의 개수가 줄어드는 것 또한 볼 수 있다.
-
-
다음 그래프는 diffF 고정비와 coverage radius에 따른 hub의 개수변화를 나타낸다.
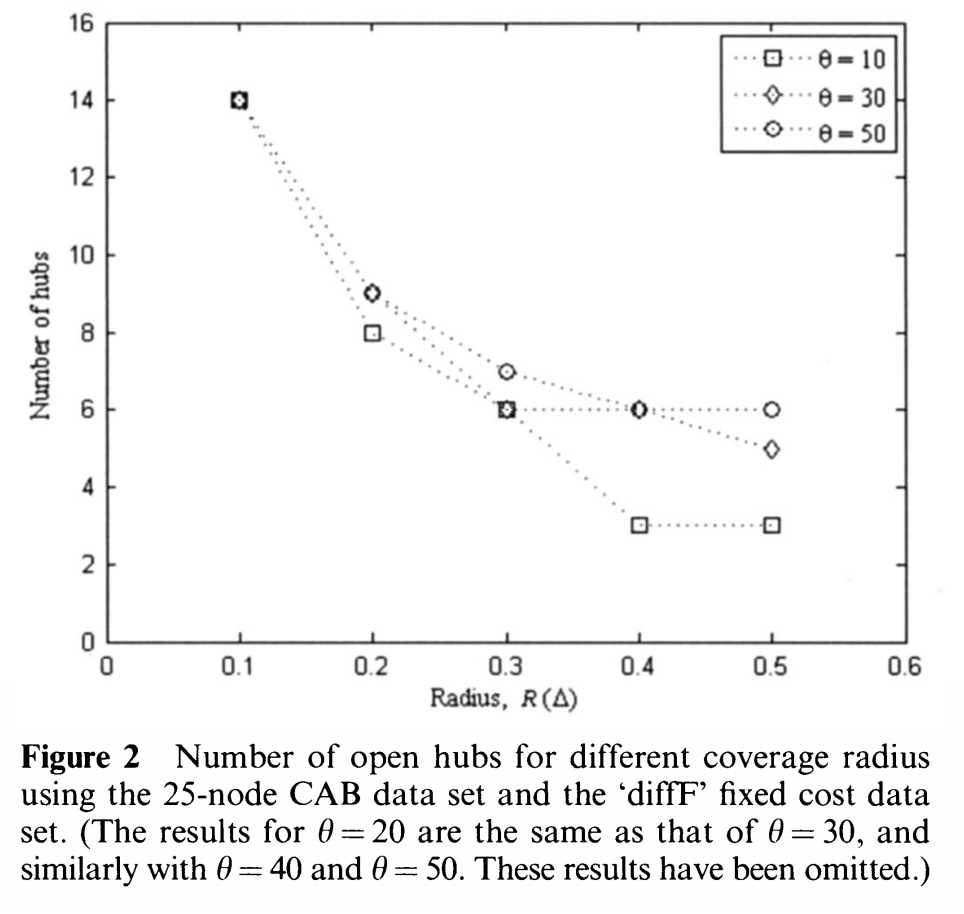
-
다음 테이블은 constF에서 hub로 선택된 노드들을 보여준다.

- 결과적으로, demand flow가 큰 노드들이 hub를 가지는 것을 볼 수 있다.
-
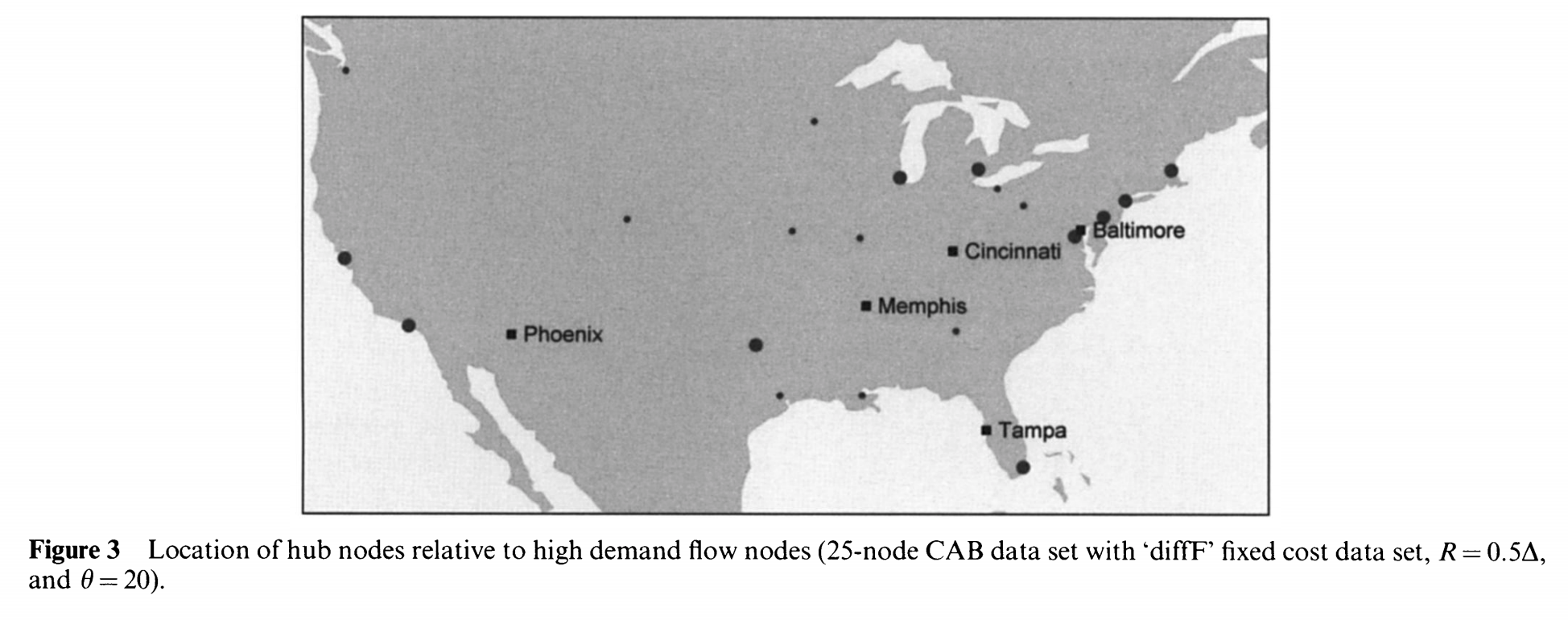
다음 테이블은 diffF에서 hub로 선정된 노드들을 보여준다.

- 여기서는, demand flow가 작은 노드지만 demand가 큰 노드와 매우 근접한 노드들이 hub가 된 것을 볼 수 있다. \(\blacksquare\)표시된 지역이 hub로 선정된 지역이다.
Multi-aircraft HCFP
HCFP에서 coverage와 관련된 parameter \(A_{ik}\)는 하나의 고정된 반지름값에 대한 것이었다.
하지만 이것을 항공사의 경우에 대입해봤을 때, 항공사는여러가지 종류의 항공기가 있고, 이러한 가정으로는 현실적인 문제를 풀 수 없게 된다.
따라서 이 논문에서는 HCFP에서 확장하여 여러가지 타입의 항공기에 대해 문제를 풀 수 있는 모델을 제시한다.
multi-aircraft HCFP에서는 목적함수에서 coverage를 충족시키지 못한 경우 패널티를 주는 방법을 사용한다. 즉, \(R_k\)가 hub \(k\)에서 출발하는 항공기의 최대 비행거리일 때, cost를 다음과 같이 재정의한다.
\[\hat{c_{ij}}= \begin{cases} c_{ik} \quad if \, 0 \leq d_{ik} \leq R_k \\ M \quad if \, d_{ik} \gt R_k \end{cases}\]이렇게 penalty를 주는 방법을 사용하면, Campbell의 origin-destination pair이 cover되는 것의 두번째 정의를 사용할 수 있다.
an origin-destination pair (ij) is covered if the length of each link in the path from node i to j through hub k first then l does not exceed a specified value.
이 두번째 정의는 hub와 non-hub간의 distance뿐만 아니라 hub끼리의 거리까지 한정한다.
따라서 hub \(k\)에 두개의 다른 항공기 종류가 있고, 각각의 cost를 \(c^1_{ik}, c^2_{ik}\)라 할때, cost는 다음과 같이 재정의될 수 있다.
\[\hat{c_{ij}}= \begin{cases} c^1_{ik}(d_{ik}) \quad if \, 0 \leq d_{ik} \leq R^1_k \\ c^2_{ik}(d_{ik}) \quad if \, R^1_k \lt d_{ik} \leq R^2_k \\ M \quad if \, d_{ik} \gt R^2_k \end{cases}\]이렇게 바뀐 cost를 목적식에 넣어 다음과 같이 바꿀 수 있고,
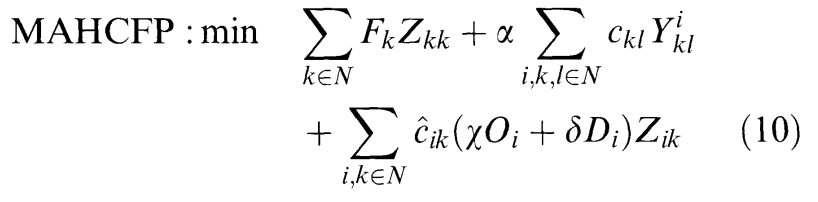
위에서 \(A_{ik}\)가 들어가던 제약식(2) 대신 다음 제약을 넣을 수 있다.
\[Z_{ik} \leq Z_{kk}, \forall i,k \in N\]이 방법 역시 MILP이며 HCFP와 규모나 구조가 거의 동일하기 때문에 문제의 복잡도 역시 유사하다.
-
아래 그래프는 diffF에서 MAHCFP를 풀었을 때, \(\tau, \beta\)에 따른 hub개수를 나타낸다.
-
\(\tau\): 더 멀리 갈 수 있는 항공기의 coverage radius
-
\(\beta\): 더 멀리 갈 수 있는 항공기의 cost의 감소량
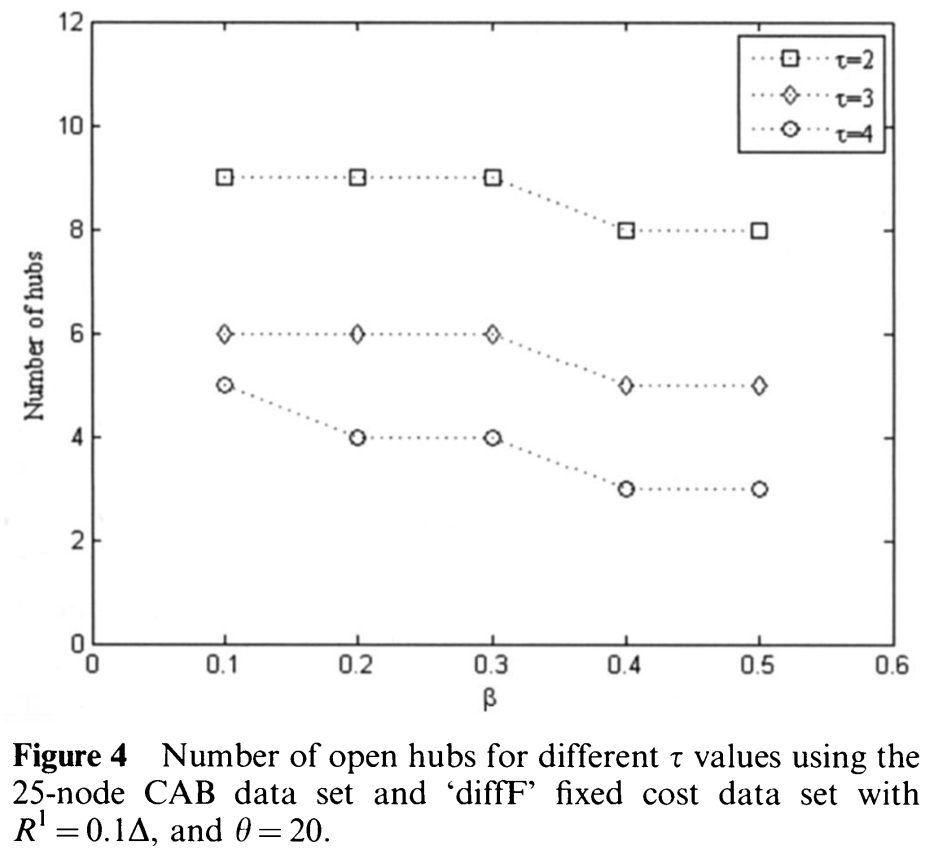
- 예상대로, \(\tau\)가 증가하거나 \(\beta\)가 늘어나면 hub의 개수가 줄어드는 것을 볼 수 있다.
-
-
다음 그래프는 zone1, zone2에 대한 그래프이다.
- zone1 : 더 짧은 거리를 가는 항공기가 커버할 수 있는 공간
- zone2 : 짧은 거리를 가는 항공기보다는 멀리 있지만, 더 멀리 가는 항공기가 커버할 수 있는 공간
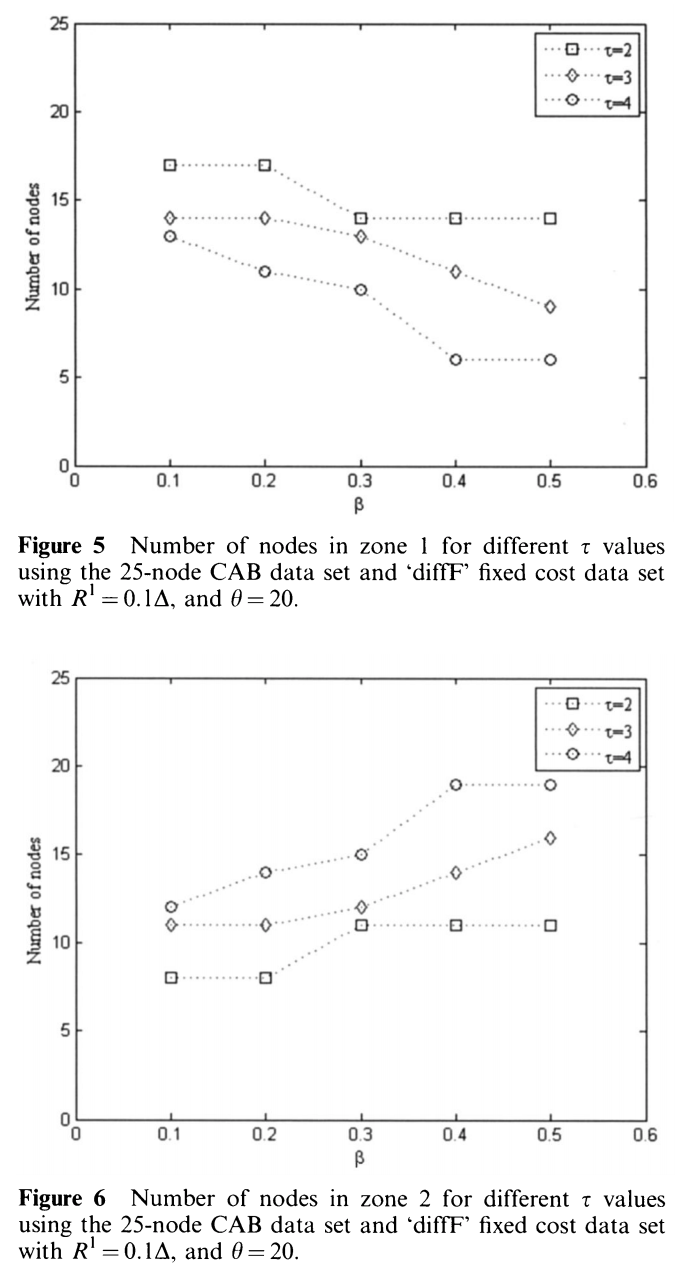
- 역시 예상대로, \(\tau\)와 \(\beta\)값이 커질수록 zone1에 속하는 노드는 줄어들고 zone2에 속하는 노드가 많아진다.
결론
-
HCFP는 hub설치 비용, demand 운송비용과 coverage제약을 고려하여 최적의 hub-and-spoke network을 찾아낸다.
-
hub노드는 고정비를 고려하여, demand flow가 많은 노드 근처에 위치하는 것이 좋다. 하지만 고정비가 모두 같다면 demand flow가 높은 곳에 위치하는 것이 좋다.
-
HCFP의 확장을 통해 multi-aircraft HCFP를 고안했다. 이를 통해 여러가지 radius를 가진 경우에 대해서도 문제를 풀 수 있었다.
-
HCFP에 capacity를 고려하는 문제도 생각해볼만 하다.