최적화 문제를 LP(Linear Programming)로 풀때, 목적함수와 제약식이 convex라면 문제는 쉽게 풀린다.

이번에는 convex라는 것이 무엇인지 알아보겠다.

convex function이란?

convex function은 아래로 볼록한 함수를 뜻한다.

이를 수학적으로 표현하자면,

Function \(f:R^n \Rightarrow R\) is called a convex function if
\(f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda) f(y)\)
for all \(x,y \in R^n\) and all \(\lambda \in [0,1]\)

이를 도식화하면 다음과 같다.

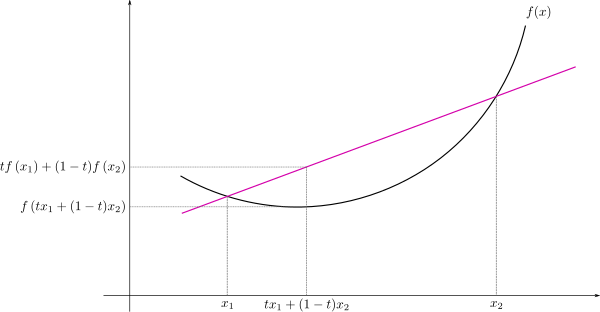
즉, x1, x2사이의 어떤 x값이 들어가더라도 함수의 결과값이 함수 위의 두 점을 잇는 선분에서의 값보다 작거나 같다면 convex function인 것이다.

그리고 convex function에 음수를 취하게 되면 concave function이 된다.

convex set이란?

convex set에 대한 수학적인 정의는 다음과 같다.

\[x_1,x_2 \in C, 0 \lt \theta \lt 1 \Rightarrow \theta x_1 + (1-\theta)x_2 \in C\]

이를 풀어 설명하면, 어떤 집합에 속하는 두 점을 이용해 선분(line segment)을 만들었을 때, 그 선분 역시 집합에 포함된다면, 이 집합을 convex라고 할 수 있다.

아래 그림을 보자.

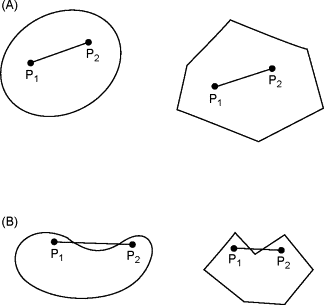
위 그림에서 (A)에 속한 두 집합은 선분을 포함하기에 convex이지만, (B)에 속한 두 집합은 선분을 포함하지 않는 경우가 있으므로 convex set이 아니다.

그렇다면 직선은 convex일까?

직선도 convex로 볼 수 있다.
convex의 정의상, 직선 위의 두 점을 잡고 선분을 만들었을 때 그 선분은 직선에 포함되기 때문이다.

사실 여기서의 선분은 convex combination으로 볼 수 있다.

convex combination이란?

수학적 정의는 다음과 같다.

\(x,y \in R^n, \lambda_1, \lambda_2 \gt 0, \lambda_1 + \lambda_2 = 1\) then \(lambda_1 x + \lambda_2 y\) is said to be a convex combination of \(x,y\)

즉, convex combination은 위 식에서 보이는 바와 같이, 집합 내 두 점을 linear combination하되, 계수가 양수이고 계수의 합을 1로 제한한 것과 같다.

이를 다음과 같이 일반화할 수 있다.

\(\sum^k_{i=1} \lambda_i x^i\), where \(\sum^k_{i=1} \lambda_i = 1\) and \(\lambda_i \gt 0, i = 1,...,k\) is a convex combination of the points \(x^1,...,x^k\)

그리고 집합 C에 포함된 모든 점들로 만든 convex combination의 집합은 convex hull이라고 한다. convex hull은 conv C라고 표기한다. conv C는 항상 convex이며 집합 C를 포함하는 가장 작은 convex set이다.

convex set과 convex function의 관계

함수 f의 epigraph가 convex set일때, 함수 f는 convex function이다.

여기서 epigraph는 함수의 그래프 위쪽 영역에 해당하는 집합이다. 따라서 supergraph라고도 한다. 이를 수학적으로 정의하면 다음과 같다.

\[epi f = {(x,\mu) : x \in \mathbb{R}^n, \mu \in \mathbb{R}, \mu \geq f(x)} \subseteq \mathbb{R}^{n+1}\]

함수 f가 convex function이라면 epi f는 항상 convex set이고, epi f가 convex set이라면 함수 f가 convex function이다

convex의 특징

업데이트 예정..

참고