우리 연구실에서는 매주 세미나를 하는데, 그 기록을 남겨두고자 블로그에도 논문 내용을 간략히 정리해서 올려보려고 한다.
이번 세미나에서 발표하게 된 논문의 제목은 A multi-objective facility location problem in the presence of variable gradual coverage performance and cooperative cover이며,
저자는 터키의 Mumtaz Karatas이다.
1. 어떤 주제의 논문인가?
이 논문은 facility location problem과 관련된 논문이다.
여기서 facility location problem은 어떤 시설이나 장비의 위치를 결정할 때 최적의 위치를 찾아내기 위한 문제를 말하는데,
일반적으로 p-median, p-center, set-covering problem, maximal covering loaction problem 등이 쓰인다.
이 논문에서는 기존의 모델들이 고려하지 못하는 여러가지 현실적인 문제들을 반영한 모델을 제안한다.
- 주요 이슈
- gradual covering decay
- cooperative coverage
- variable coverage performance
- multi-objective location planning
그리고 이 논문에서는 후보지의 위치가 미리 정해져있는, discrete한 조건을 가진 위치선정문제를 다룬다.
2. 이런 부분을 반영하고자 하는 이유가 있나?
좀 더 현실을 반영한 모델을 만들기 위함이다. 현실을 충실히 반영하지 못한 모델은 쓸 수 없기 때문이다.
그렇다면 이 논문에서 이슈로 삼고 있는 각각의 문제들에 대해 살펴보자.
-
gradual covering decay
-
현실의 여러 설비, 장치들은 거리에 따라 그 성능이 줄어드는 경우가 많다.
-
예를 들어, 감지 센서, 의료 시설, 등대, WI-FI, 신호 수신기 등 많은 설비들이 그러하다.
-
-
cooperative coverage
-
하나의 customer이 꼭 하나의 설비에게서만 서비스를 받을 필요는 없다.
-
여러개의 설비가 하나의 customer에게 동시에 서비스 제공하는 경우도 충분히 존재한다.
-
예를 들어, 경보 사이렌, 송신탑, 감시 센서 등이 그러하다.
-
-
variable coverage performance
-
현실의 많은 설비들은 그 사이즈에 따라 커버할 수 있는 반경과 capatity가 달라진다.
-
그리고 설비들은 사이즈에 따라 cost가 달라진다.
-
-
multi-objective location planning
-
현실의 의사결정권자는 바라는게 하나가 아니다.
-
가격, 서비스의 질, 이동 시간, 작업부하의 균형 등을 동시에 고려하는 모델이 필요하다.
-
그리고 각 요인들은 대개 상충관계에 있다.
-
3. 이 문제들을 어떻게 풀었나?
수리모형을 통해 문제를 해결했다.
기본적으로 multi-objective integer non-linear program(INLP)을 이용해 문제를 풀었고,
network 구조를 이용해서 INLP를 multi-objective integer linear program(ILP)로 표현하여 시간은 좀 더 소요되지만, 더 좋은 솔루션을 얻어냈다.
최종적으로는 그 두개를 합한 combined INLP-ILP를 만들어 짧은 시간 안에 좋은 솔루션을 얻을 수 있게 되었다.
4. 가정과 전제조건은?
4.1 Modeling gradual cover
-
일반적인 deterministic coverage model은 설비의 커버 반경이 정해져있다. 그리고 그 반경 안에 들어오는 customer은 확정적으로 cover되지만 그 밖에 있다면 전혀 영향을 받지 않는다.
-
하지만 이 논문에서는 gradual cover 개념을 도입해 위의 가정을 완화(relaxation)한다.
-
각 demand마다 \(\bar{d}\)(minimum critical distance)와 \(\bar{\bar{d}}\)(maximum critical distance)을 정의한다.
-
설비가 어떤 demand의 \(\bar{d}\)안에 존재 한다면 그 demand는 완전히 cover된다.
-
만약 어떤 demand의 \(\bar{\bar{d}}\)안에 설비가 존재하지 않는다면 demand는 cover되지 않는다.
-
만약 어떤 demand의 \(\bar{d}\)와 \(\bar{\bar{d}}\) 사이에 설비가 존재한다면 그 demand는 부분적으로 cover된다.
-
-
demand와 설비간의 거리에 따른 커버 수준에 대한 함수는 Fermi-type coverage model을 채택했다. 그 식은 다음과 같다.
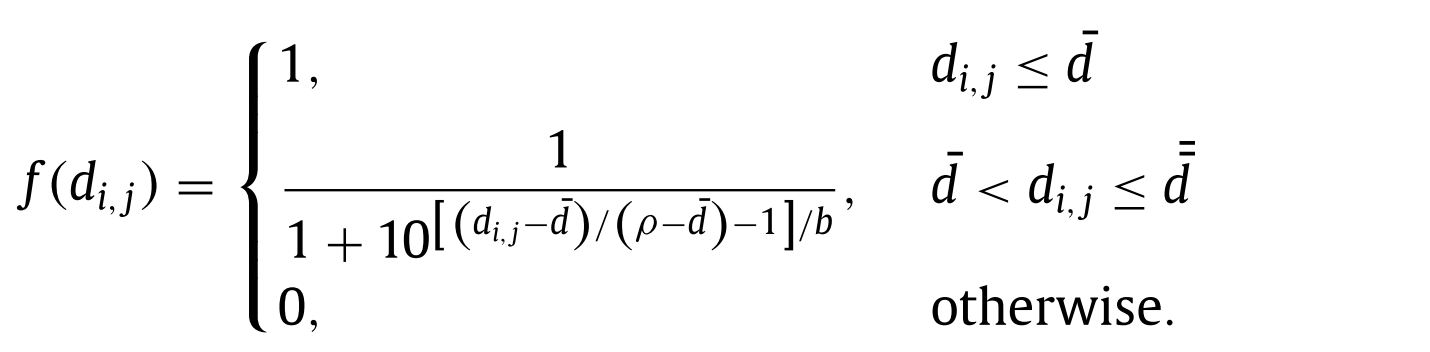
- \(d_{i,j}\) : demand \(i\)와 설비 \(j\)간의 거리
- \(b\) : 함수의 ‘tailing’ 특성에 관한 sensitivity 파라메터
- \(\rho\) : \(\bar{d}\)보다 크며, 커버 확률이 정확히 반반이 되는 range를 의미한다.
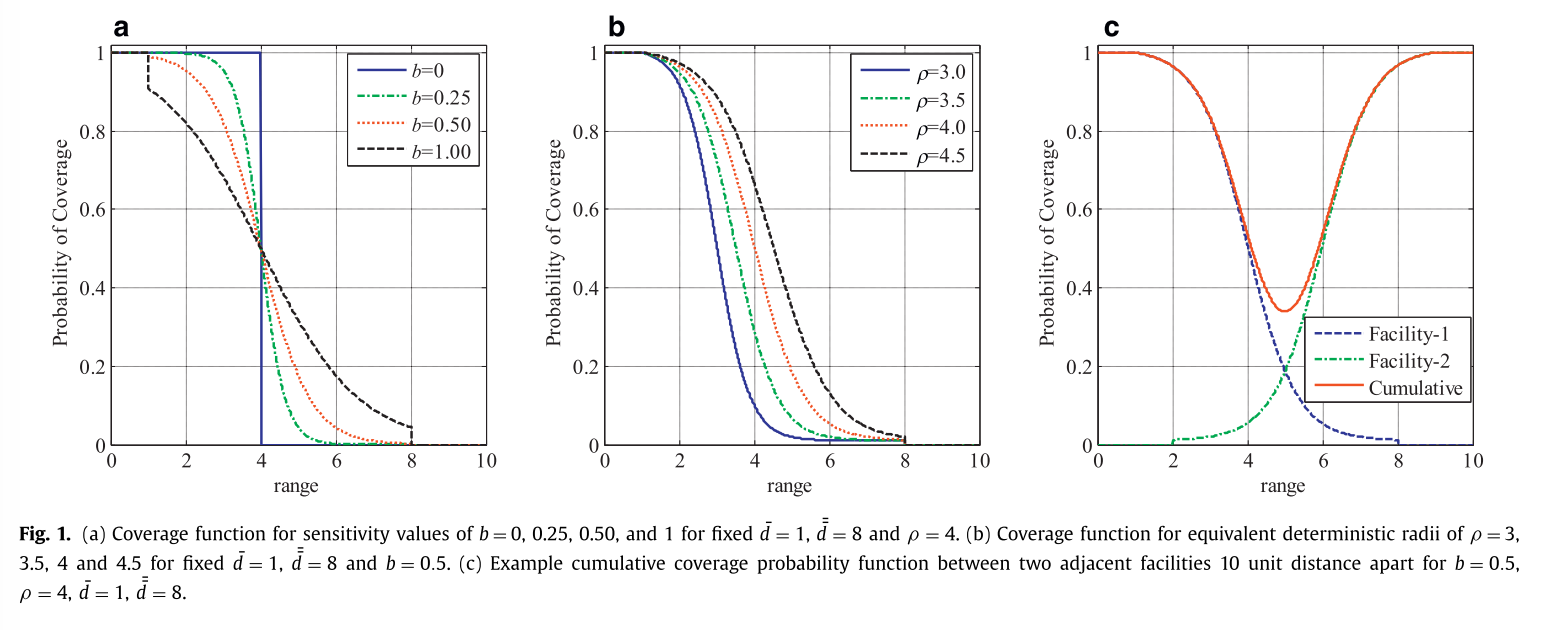
- 위 그래프는 파라메터에 따라 함수가 어떻게 변하는 지 보여준다.
- (a)는 \(b\)의 값에 따른 함수의 모습을 보여준다. 이때 \(b\)의 값이 0이라면, deterministic model과 같은 것을 볼 수 있다.
- (b)는 \(\rho\)의 값에 따른 함수의 모습을 보여준다.
- (c)는 두개의 설비에 대해서 demand가 커버될 확률을 누적그래프로 보여준다.
4.2 Modeling variable coverage performance and size
-
이러한 커버 문제에서는 대개 constant한 커버 성능(performance)을 가정하고, 그것은 의사결정 권한 밖의 것으로 생각한다.
-
하지만 앞서 언급했듯, 설비의 커버 반경은, 현실의 많은 경우와 같이, 설비의 물리적인 크기(size)에 영향을 받는다. 따라서, 논문에서도 이를 가정했다.
-
그래서 논문은 variable coverage performance와 gradual cover을 동시에 고려한다.
-
이때, 설비의 커버 반경은 discrete하다. 미리 정해져있는 set안에서 반경이 정해진다.
-
이를 고려하여, 기존의 \(\rho\) 대신 설비별 커버 반경 \(r\)을 고려한 \(\rho_r\)이 fermi function에 들어가게 된다.
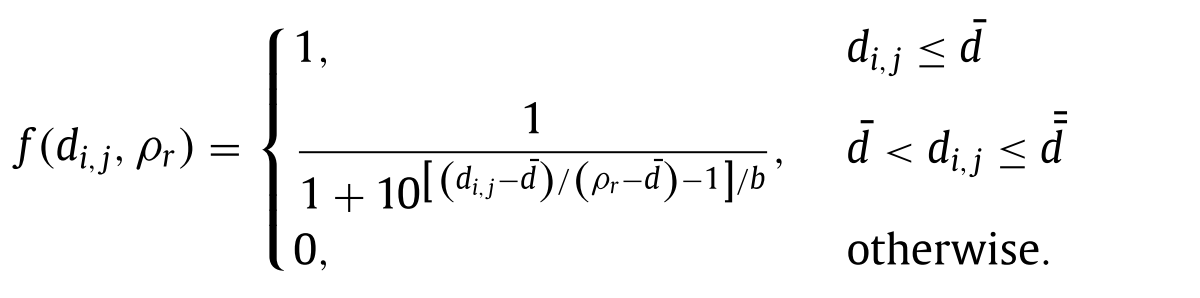
- 그래프 (b)에서 보았듯, \(\rho_r\)값이 커지게 되면 커버될 확률이 커지게 된다.
-
설비의 size는 \(\rho_r\)에 비례하고, 다음과 같은 식으로 계산될 수 있다.
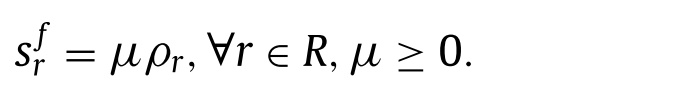
- \(s^f_r\) : 커버 반경 \(\rho_r\)을 갖는 설비의 크기
- \(s^{cl}_j\) : 후보지 \(j\)의 물리적인 크기
-
이때, feasibility를 유지하기 위해 모든 설비들에 대해 \(s^f_r \leq s^{cl}_j\)은 만족해야한다.
4.3 Modeling cooperative coverage
-
대부분의 입지선정 모델에서는 가장 가까운 설비 하나가 demand를 충족시키지만, 이 논문에서는 다수의 설비가 동시에 하나의 demand를 커버할 수 있도록 했다.
-
여기서, 각 설비의 커버는 다른 설비들의 커버에 대해 독립적인 것으로 가정한다.
-
따라서, 어떤 demand가 충족되지 못할 확률은 각 설비들이 그 demand를 충족하지 못하는 확률들의 곱으로 표현될 수 있다.
-
\((j,r)\)이 장소 \(j\)에 반경 \(r\)인 설비일 때, \(K\)를 \((j,r)\) 쌍들을 포함하는 집합이라고 하자. (\(K \subset J \times R\))
-
이때, demand \(i\)의 누적 커버 확률 \(P_i\)는 다음과 같은 식으로 표현된다.
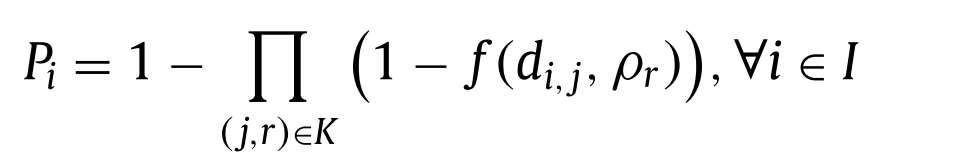
-
위 그래프 (c)를 보면, 여러개의 설비가 커버할 때 전체적인 커버 성능이 높아지는 것을 볼 수 있다.
4.4 Multiple objectives
-
논문에서는 세가지 사항을 고려한다.
- Coverage
- Cost
- Workload Balance
-
각 목적마다 중요한 정도가 미리 정해져있다고 가정한다.
-
Goal programming 개념을 이용해서, 모든 목적을 하나의 목적식으로 변환한다.
-
모든 목적(Goal)의 집합 \(G\)에 대해 \(g \in G\)라 할때, 각각의 요소 \(g\)에 대해 의사결정권자는 가중치 \(w_g\)를 매긴다.
4.4.1 \(\alpha\)- coverage
-
이 목적은 미리 정해놓은 커버 분기점(threshold) \(\alpha\) 안에서 demand가 커버될 확률로 정의된다.
-
이 논문에서는 각각의 demand마다 커버 requirement가 다르다고 간주했다. 따라서, 각각의 demand \(i\)에 대해 coverage level \(\alpha_i\)를 정의하고 \(\alpha\)-coverage 개념을 다음과 같이 정의했다.

-
\(\alpha\)값은 의사결정권자가 설정한다. \(\alpha\)값이 클 수록 가깝고 큰 설비를 선호하게 된다.
-
목적식에서 각 target \(\alpha\)값과의 음(negative)의 편차를 최소화한다. 이 방법으로 infeasible을 방지하되, 가능한 높은 \(\alpha\)-coverage를 유지할 수 있게 해준다.
4.4.2 Budget
-
이 논문에서 cost는 다음과 같이 정의하였다.
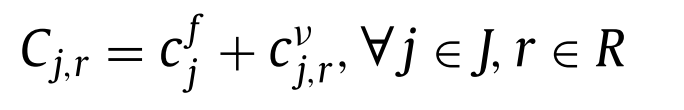
- \(j\) : 설비 위치
- \(\rho_r\) : 설비 커버 반경
- \(c^f_j\) : 고정비
- \(c^v_{j,r}\) : 변동비
-
변동비는 non-decreasing function으로, 다음과 같이 정의하였다.
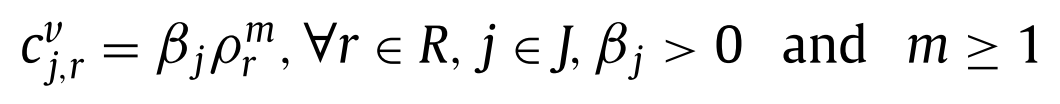
-
\(\beta_j\)는 위치별로 달리 주어지는 상수
-
\(\rho^m_r\)에서 m은 marginal return curve를 결정한다. \(m \gt 1\) 일 경우 increase, \(m \lt 1\) 일 경우 decrease이다.
-
-
Budget 차원에서, 목적함수는 cost와 주어진 예산 \(B\)사이의 양(positive)의 편차를 최소화 한다.
4.4.3 Workload Balance(Capacity)
-
많은 입지선정 모델들은 설비의 capacity에 제한을 두지 않아 demand를 무제한으로 충족할 수 있다. 하지만 이는 현실의 상황에는 맞지 않다.
-
이 논문에서는 capacity역시 설비의 size에 따라 커진다고 가정하고, 설비의 커버반경 \(r\)에 따른 capacity를 다음과 같이 정의했다.
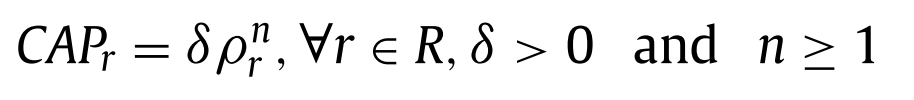
- \(CAP_r\) : 어떤 설비의 커버반경이 \(r\)일때, 그 설비의 capacity
- \(\delta\) : 상수
-
목적함수에서 capacity는 workload와 비교되어 그 편차를 줄이는 데 쓰인다. 설비 용량에 제약을 둠과 동시에 workload balancing의 도구로 쓰이는 것이다.
5. Model Formulation
논문에선 앞서 설명한 내용들을 바탕으로 수리모델을 만들었다.
5.1 Multi-objective integer non-linear programming (INLP) formulation
-
Sets and indices

-
Parameter

-
Decision variables

-
Objective function
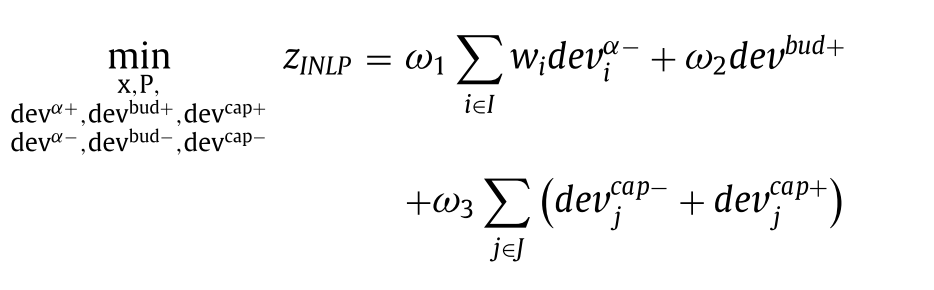
-
Constraints
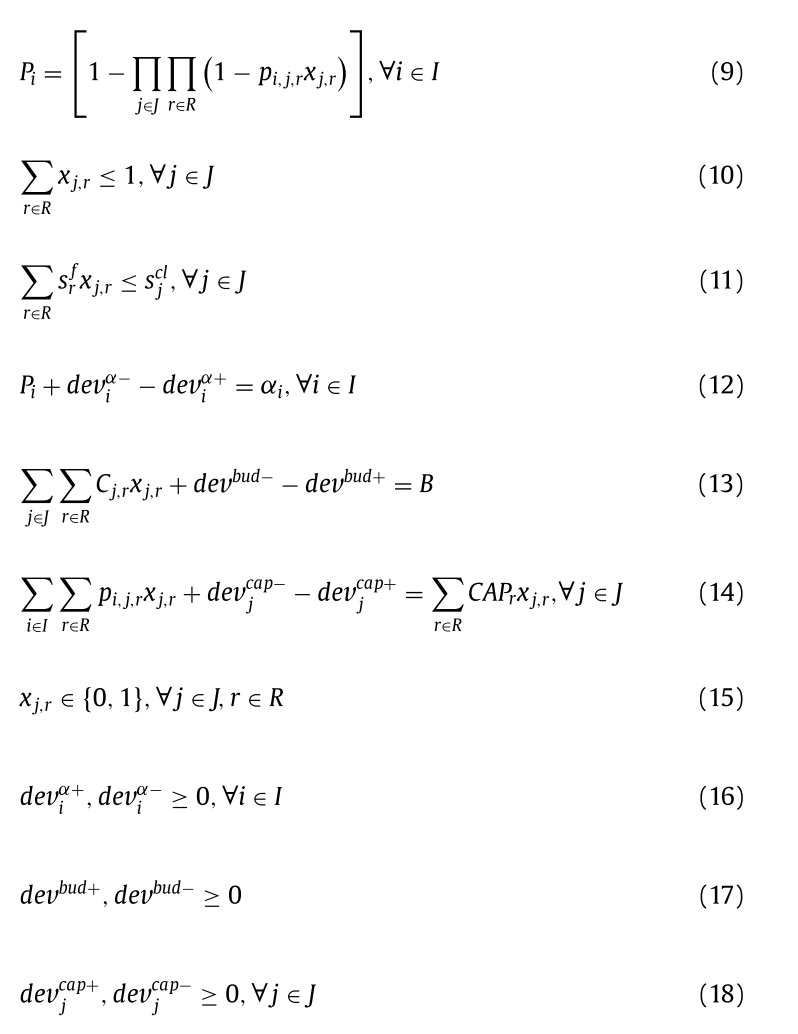
-
(9)번 제약식은 누적 커버 확률을 정의한다.
-
(10)번 제약식은 한 장소에 최대 하나의 종류의 설비만이 설치될 수 있도록 한다.
-
(11)번 제약식은 설비의 물리적인 크기가 해당 위치의 크기보다 클 수 없도록 한다. \(s^f_r\)은 설비 크기를 설명하면서 정의한 바 있다.
-
(12)번 제약식은 커버수준에 대한 편차를 정의한다.
-
(13)번 제약식은 예산의 편차를 정의한다.
-
(14)번 제약식은 capacity의 편차를 정의한다. 이는 목적함수에서 workload balance를 맞추는 데 활용된다.
-
(15)번부터 (18)번 제약식은 변수 타입을 정의한다.
-
5.2 Multi-objective integer linear programming (ILP) formulation
-
INLP 모델은 convexity를 보장하지 않기 때문에 global optimal을 보장하지 못한다.
-
따라서 이 논문에서는 네트워크 개념을 도입하여 INLP를 linearize(선형화)한 ILP 모델을 소개한다.
-
이 방법은 경로를 따라 flow를 커버 확률을 capture하는 flow를 만드는 네트워크를 사용한다.
-
그러기 위해서, 새로운 decision variable로 transitory non-coverage probability변수를 정의하고, 제약식을 추가한다.
-
이해를 돕기위해 논문의 그림을 살펴보자.
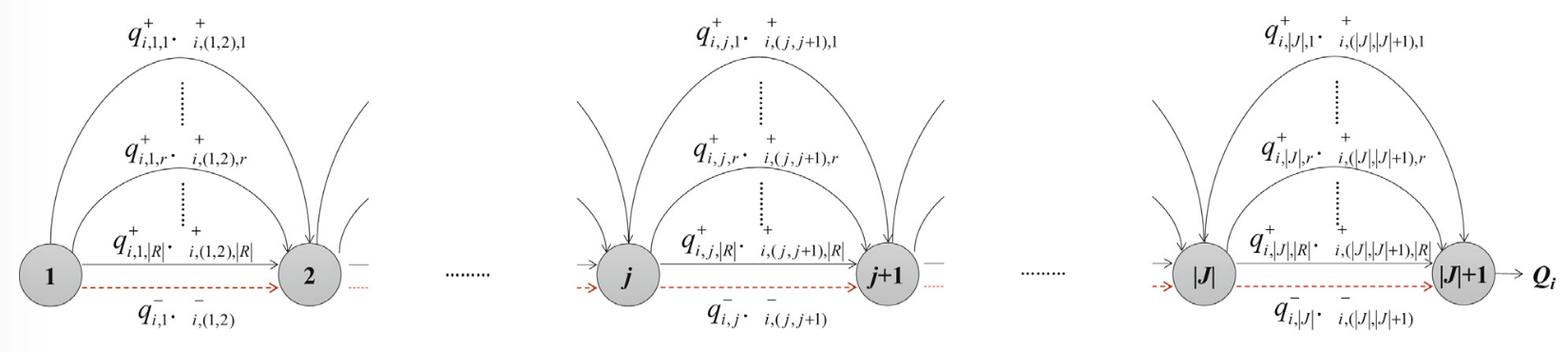
-
위 그림은 하나의 demand \(i\)에 대한 flow를 보여준다. 각 demand에 대해 flow는 그 demand가 arc에 대해 커버되지 않을 확률을 나타낸다.
-
네트워크의 각 노드는 임의의 후보지 \(j \in J\)를 나타낸다.
-
각각의 네트워크 링크는 \(\mid R\mid+1\)개의 평행한 아크로 구성된다.
-
특히, 인접한 (adjacent)노드끼리는 \(r \in R\)에 대해 positive labeled arc이 있고, 하나의 negative labeled arc가 존재한다.
positive labeled arc : \(x_{j,r} = 1\)이라면, 설비 크기가 \(r\)이고 나가는 노드가 \(j\)인 positive labeld arc에 flow가 발생한다.
negative labeled arc : 위치 \(j\)에 어떤 설비도 설치되지 않는다면, negative labeled arc에 flow가 발생한다.
-
이 아크들은 demand \(i\)의 전체적인 non-coverage probability와 관련하여 flow의 평가 기준이 된다.
-
전체 flow의 양은 flow가 최종 노드 \(\mid J \mid+1\)로 향하면서 유지되거나 줄어들어야 한다.
-
이때, 아크를 지나는 flow의 양을 뜻하는 변수(transitory non-coverage probability) \(\pi^{+}_{i,(j+1),r}\)과 \(\pi^{-}_{i,(j+1),r}\)이 사용된다.
-
게다가, \(x_{j,r} = 1\)이라면 노드 \(j\)를 떠나는 flow가 \(q^{+}_{i,j,r}\)의 비율만큼 scale down 된다. 반대로, \(x_{j,r} = 0\) 이라면, flow는 그래로 유지되며, \(q^{-}_{i,j} = 1\)이다.
\(q^{+}_{i,j,r}\) : \(j\)위치의 커버 반경 \(r\)을 갖는 설비가 demand \(i\)를 커버하지 못할 확률. 즉, \(q^{+}_{i,j,r} = 1 - p_{i,j,r}\)
-
\(\mid J \mid +1\) 노드는 가상의 노드이며, 이는 demand \(i\)에 대한 총 flow양 \(Q_i\)를 의미하게 된다.
-
-
Additional parameter

-
Additional Decision Variable

-
Constraints
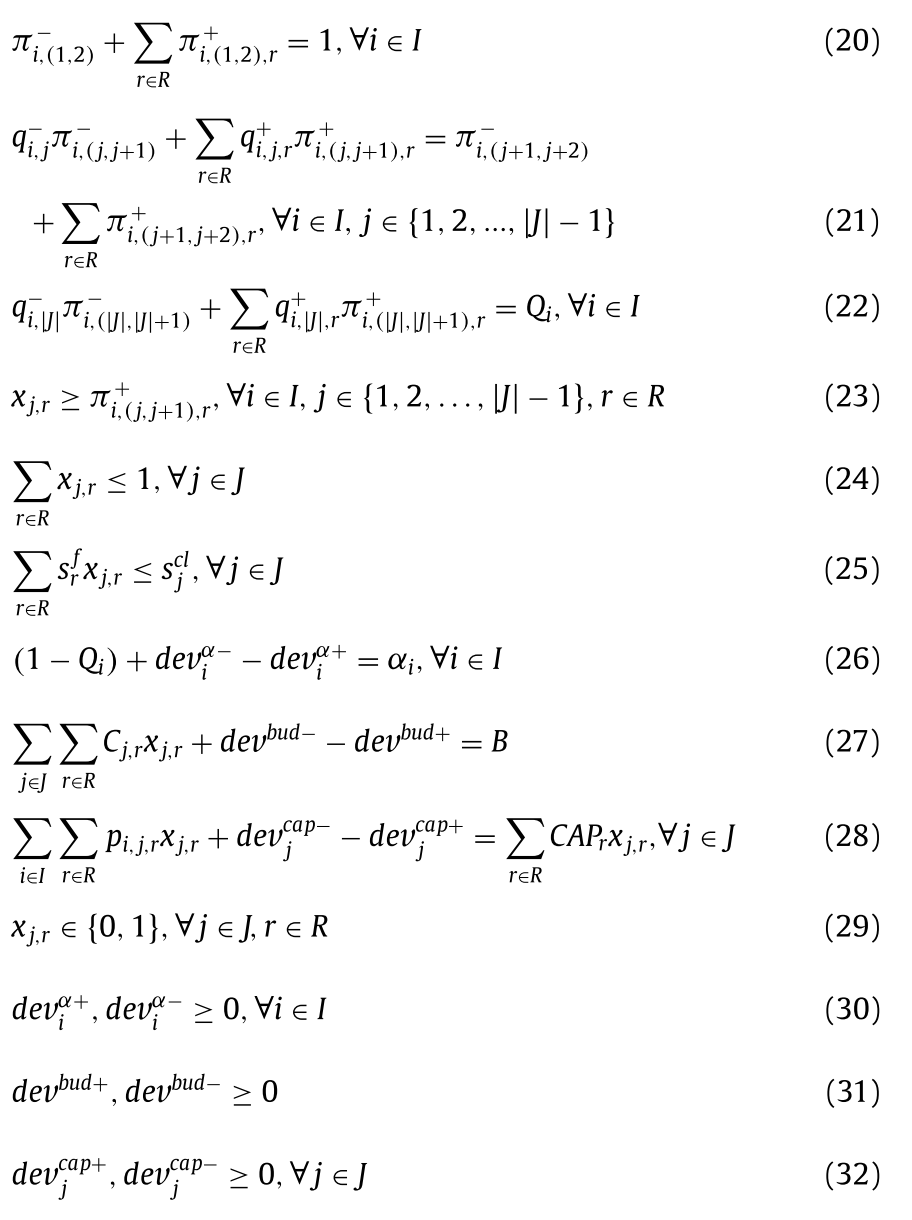
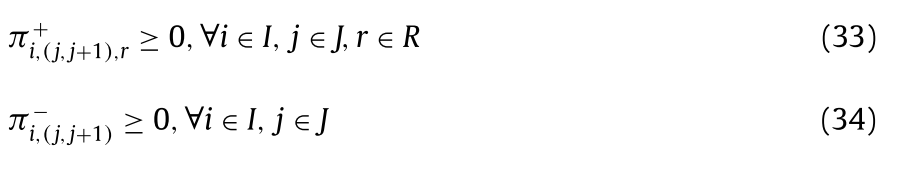
-
(20)번 제약식은 각 demand의 첫번째 노드에서의 flow양의 총합(transitory non-coverage probabilities)을 1로 만들어 주어 flow를 초기화시켜준다.
-
(21)번 제약식은 flow-balance제약식이다. 들어오는 scaled flow와 나가는 unscaled flow를 맞춰준다.
-
(22)번 제약식은 \(\mid J \mid\)번째 노드에서 나와서 \(\mid J \mid +1\)노드로 들어가는 flow의 합을 통해 demand \(i\)의 최종 non-coverage probability \(Q_i\)를 계산한다.
-
(23)번 제약식은 (29)번 제약식과 함께 \(\pi^{+}_{i,(j,j+1),r}\)이 양수일 경우 \(x_{j,r}\)의 값이 1이 될 수 있도록 한다.
-
5.3 Combined INLP-ILP solution procedure
-
ILP는 global optimal을 보장하지만 시간이 너무 오래걸린다.
-
Genetic Algorithm, Simulated Annealing과 같은 메타휴리스틱 기법도 쓸 수는 있지만, 솔루션의 퀄리티를 보장할 수는 없다.
-
그래서 이 논문에서는 INLP와 ILP를 합치는 방법을 소개한다.
-
이 방법은 ILP를 시작할 때 solution space에서 좋은 시작점을 제공한다. 따라서 global optimal을 보장하면서 계산 시간은 짧은 것이다.
-
즉, \(x^*\)을 INLP의 최적해라고 할 때, \(x^*\)의 정보를 ILP 모델의 시작점으로 사용하는 것이다.
Experiments
-
실험은 소형,중형,대형 사이즈의 데이터에 대해 이뤄졌으며, 각 사이즈에 대해 demand 개수 \(\mid I\mid\), 후보지 개수 \(\mid J\mid\), 가능한 설비 커버 반경 개수 \(\mid R\mid\)을 설정했다. 총 36개의 조합에 대해, 50개의 랜덤 데이터를 생성하여 실험을 진행했다.
-
자세한 파라메터에 대한 정보는 다음 테이블에 정리되어있다.

-
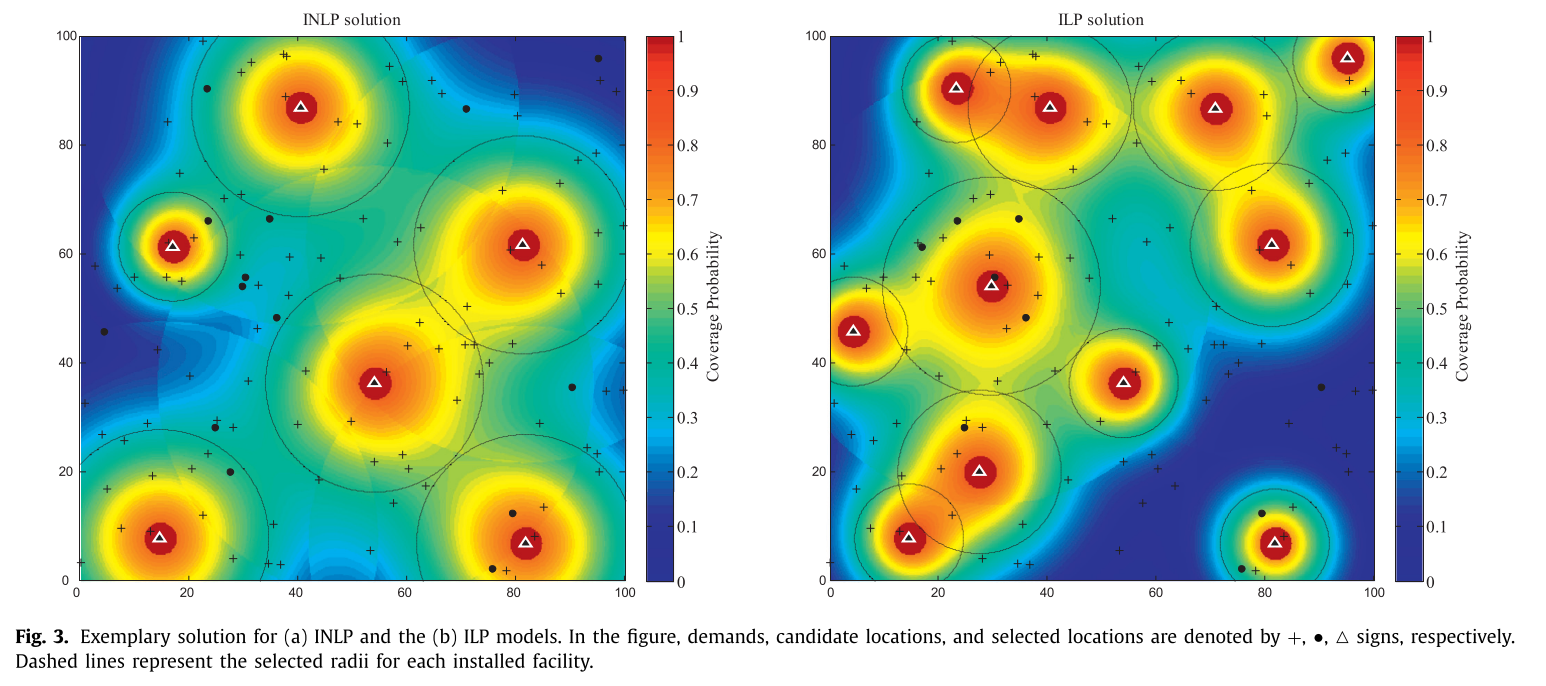
다음은 INLP와 ILP에 대한 솔루션 예시다.
-
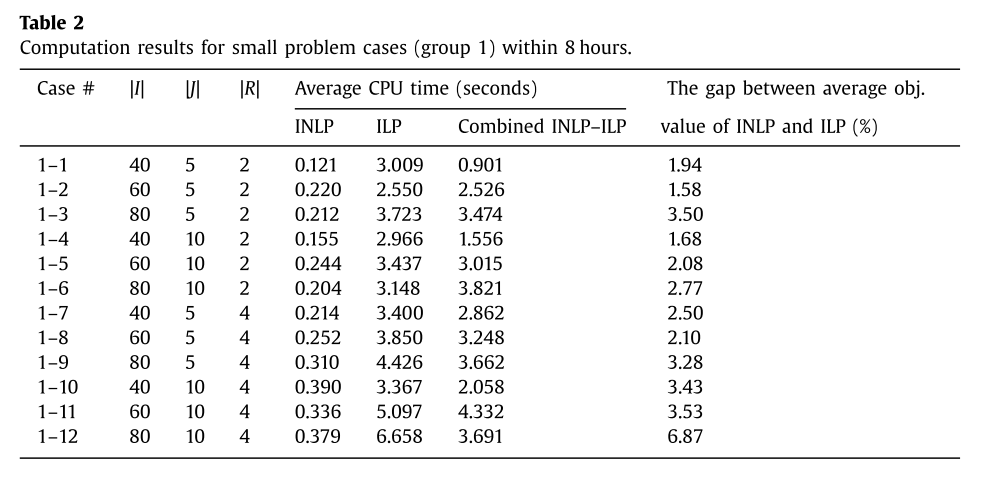
group 1에 대한 실험 결과는 다음과 같다.
-
INLP는 모든 실험에서 속도와 솔루션 퀄리티 모두 좋았다.
-
INLP와 ILP간의 objective value가 7% 미만이었다.
-
ILP는 2~7초 정도 시간이 더 걸리지만 global optimal을 보장한다.
-
INLP-ILP 혼합 모델은 ILP와의 optimality gap이 0 이었고, 풀이 속도는 더욱 빨랐다.
-
-
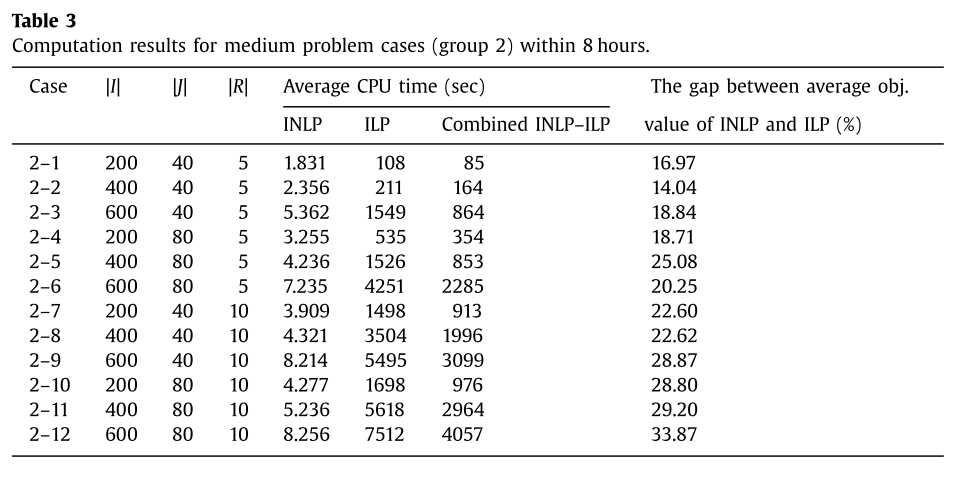
group 2에 대한 실험 결과는 다음과 같다.
-
INLP는 1~9초 내에 내에 문제를 풀지만 gap이 14%~34%나 된다.
-
ILP는 문제 사이즈에 따라 2~125분만에 문제를 풀었다.
-
INLP-ILP 혼합 모델은 ILP에 비해 약 40% 빠르게 문제를 풀 수 있었다.
-
-
group 3에 대한 실험 결과는 다음과 같다.
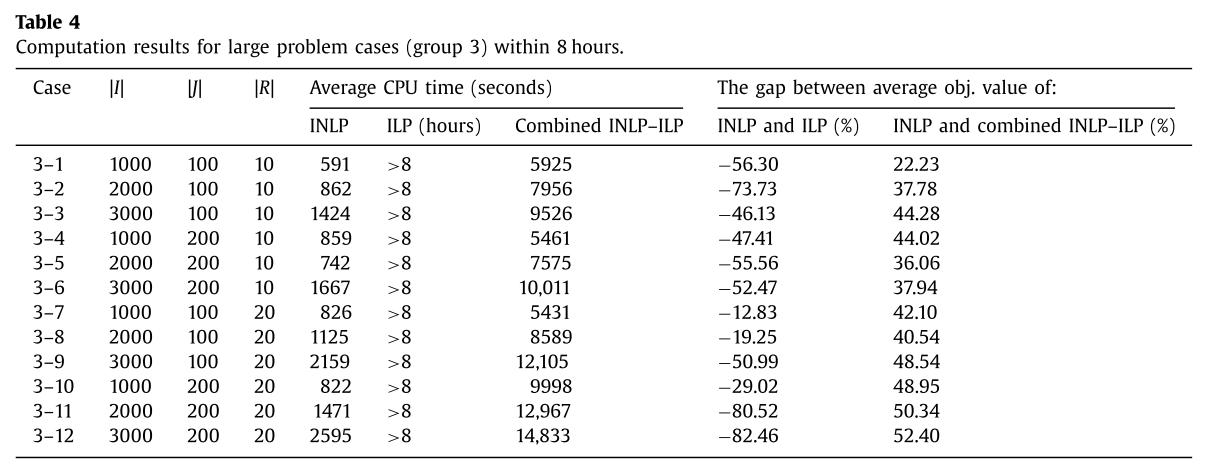
-
ILP는 시간 제한인 8시간을 넘겨 문제를 끝까지 풀지 못했으며, INLP보다 솔루션이 좋지 못했다.
-
INLP는 10~44분만에 문제를 풀었으며, ILP에 비해 12%~83% 좋은 솔루션을 보여줬다.
-
INLP-INL 혼합 모델은 평균 2.5시간 내에 global optimal을 찾았다. 그리고 INLP와의 gap은 22%~53%였다.
-
-
각 방법에 따른 계산 시간 그래프는 다음과 같다.
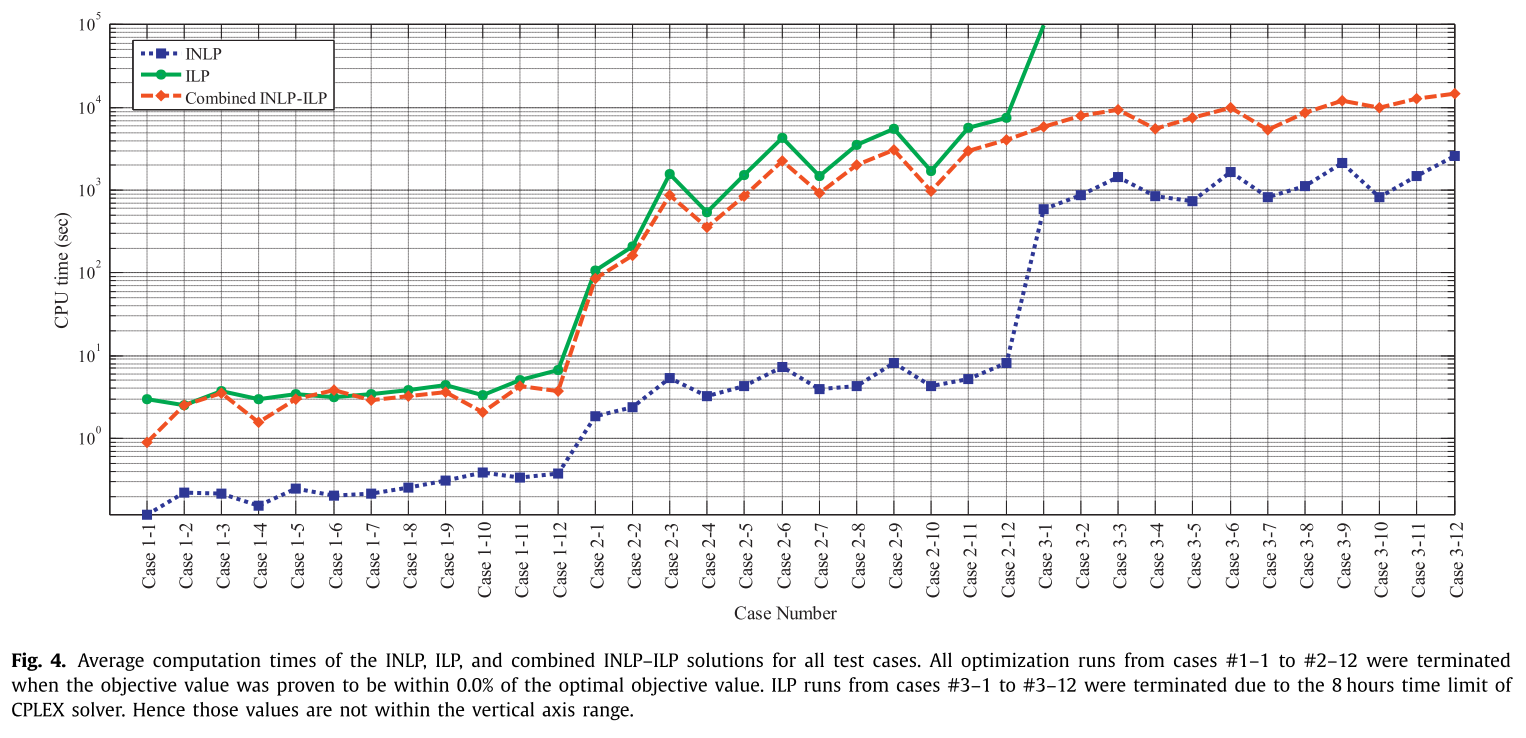
- 그래프가 log 함수의 형태를 띄는 것을 볼 수 있다.
-
INLP-ILP와 INLP의 gap에 대한 그래프는 다음과 같다.
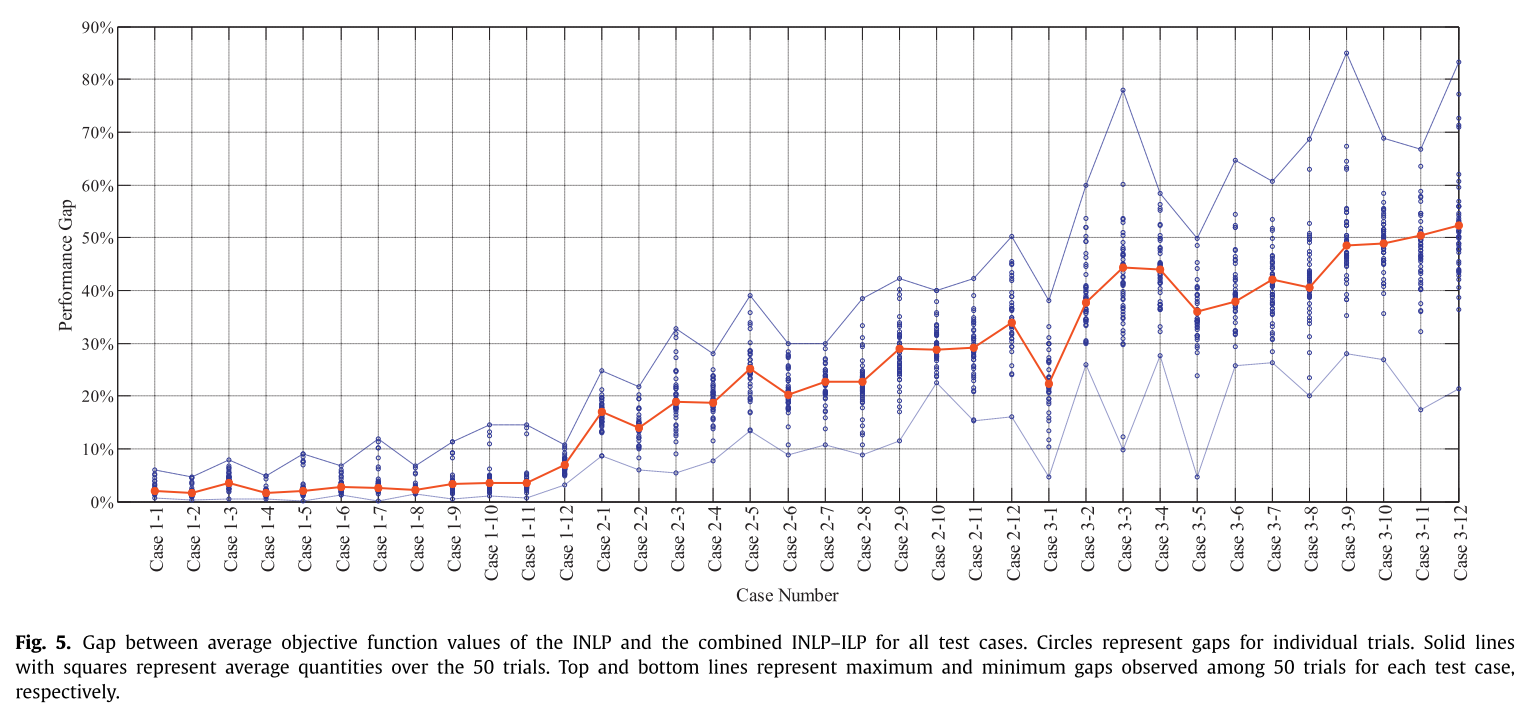
- 문제 사이즈가 커질수록 gap이 커지는 것을 볼 수 있다.
Conclusion
-
이 논문은 gradual covering decay, cooperative demand coverage, user-defined variable coverage performance와 같은 현실의 다양한 조건들을 동시에 반영했다.
-
의사결정권자가 설정한 파라메터에서 편차를 최소화 하는 multi-objective 모델을 만들었다.
-
Non-linear한 문제를 network와 유사한 구조를 이용하여 linearize하여 문제를 효율적으로 풀었다.
-
Non-linear문제와 linear문제를 조합하여 빠르게 global optimal을 찾아내는 모델을 만들었다.