이번 학기부터 학과조교로 근무를 하게 되면서 학부조교들의 근무 일정을 짜야하는 상황이 생겼다.
20명이나 되는 사람들의 시간표를 일일이 대조하면서 적절하게 스케줄링을 해줘야 했는데, 수작업으로 하기에는 실수도 많을 것 같고 효율적이지 않아보였다.
게다가 매 학기 이 작업을 일일이 해야한다고 생각하니 벌써부터 귀찮았다.
그래서 최적화 모델을 만들어서 좀 더 스마트하게(?) 스케줄을 짜기로 했다.
기본조건
- 장소 : 사무실, 실험실, 스터디룸
- 장소별 시간 : 1~12교시
- 요일 : 월~금
- 학생 : 20명
- 근무시간 : 10명씩 각각 10시간, 5시간
- 시간,장소당 최대 근무 인원 : 2명
- 시간,장소당 최소 근무 인원 : 1명
추가조건
- 사무실에는 금요일 근무가 없다.
- 사무실에는 3~4교시 근무가 없다.
- 사무실 근무는 1~8교시까지만 한다.
- 사무실의 2교시 근무는 한사람당 한번만 할 수 있다.
- 사무실 근무는 하루 2시간만 배정한다.
- 5교시 이후 사무실 근무는 1번만 있으면 된다.
- 사무실 근무는 1명씩만 근무한다.
- 실험실에 수업이 있는 시간에는 근무가 없다.
- 학생이 공강인 요일에는 최대한 배려해서 해당 요일에는 근무를 만들지 않는다.
- 근무는 최대한 연달아서 할 수 있게 해준다.
Parameter
- \(S \in \{0..19\}\) : 학생
- \(T \in \{0..11\}\) : 시간(교시)
- \(D \in \{0..4\}\) : 요일
- \(P \in \{0..2\}\) : 장소
- \(Avail_{s,t,d}\) : \(s\)학생이 \(d\)요일 \(t\)시간에 근무가 가능하다면 1, 아니면 0
- \(Limit_{t,d,p}\) : \(d\)요일 \(t\)시간 \(p\)장소에 최대 근무가능 인원
- \(Req_{t,d,p}\) : \(d\)요일 \(t\)시간 \(p\)장소에 최소 근무 인원
- \(AssignTime_{s}\) : 학생 \(s\)가 근무해야하는 총 시간
- \(\lambda_{t}\) : 시간 \(t\)에 따른 가중치 (늦은 시간에는 최대한 적은 인원이 근무할 수 있도록)
Decision Variable 결정변수
- \(w_{s,t,d,p}\) : \(s\)학생이 \(d\)요일 \(t\)시간에 \(p\)장소에서 근무한다면 1, 아니면 0
- \(sw_{s,t,d,p}\) : \(s\)학생이 \(d\)요일 \(t\)시간과 \(t+1\)시간에 \(p\)장소에서 연속적으로 근무한다면 1, 아니면 0
Objective 목적식
- 총 근무의 합을 구하고 연속된 근무를 최대한 만들 수 있도록 \(sw_{s,t,d,p}\) 의 계수는 음수로 하여 \(Min\) 문제를 푼다.
- \[Min \quad \sum_{s}\sum_{t}\sum_{d}\sum_{p}\lambda_{t}w_{s,t,d,p} - \sum_{s} \sum_{t \in {1..11}} \sum_{d} \sum_{p}sw_{s,t,d,p}\]
Constraint 제약식
- \[\sum_{t} \sum_{d} \sum_{p}{w_{s,t,d,p}} = AssignTime_{s} \quad ,\forall s \in S\]
- \[\sum_{p} w_{s,t,d,p} \leq Avail_{s,t,d} \quad ,\forall s \in S, t \in T, d \in D\]
- \[\sum_{s} w_{s,t,d,p} \leq Limit_{t,d,p} \quad ,\forall t \in T, d \in D, p \in P\]
- \[\sum_{s} w_{s,t,d,p} \geq Req_{t,d,p} \quad ,\forall t \in T, d \in D, p \in P\]
- \[\sum_{s} \sum_{t \in \{4..11\}} w_{s,t,d,0} = 1 \quad ,\forall d \in D\]
- \[2sw_{s,t,d,p} \leq w_{s,t,d,p} + w_{s,(t+1),d,p} \quad ,\forall s \in S, t \in T, d \in D, p \in P\]
- \[\sum_{d} w_{s,1,d,0} \leq 1 \quad ,\forall s \in S\]
- \[\sum_{p} w_{s,t,d,0} \leq 1 \quad ,\forall t \in T, d \in D\]
- \[\sum_{s}\sum_{p \in \{1,2\}} sw_{s,t,d,p} \geq 1 \quad ,\forall t \in {8..10}, d \in D\]
각 제약식의 의미
1. 각 학생들은 정확히 자신에게 할당된 시간만큼 근무해야한다.
2. 각 학생들은 근무가 불가능한 시간이 있다.
3. 한 근무에 대해서 최대 인원이 있다.
4. 한 근무에 대해서 최소 인원이 있음.
5. 사무실에서는 5교시 이후 1시간만 근무한다.
6. 연속으로 두시간 일하는 경우
7. 사무실 2교시 근무는 1인 최대 1번이다.
8. 사무실 근무는 한 명씩만 한다.
9. 9교시 이후 근무는 늘 연속되야한다.
Data 데이터
- 학생별로 근무가능 시간에 대한 데이터는 CSV파일로 따로 정리해서 넣어두었다.
- avail.csv
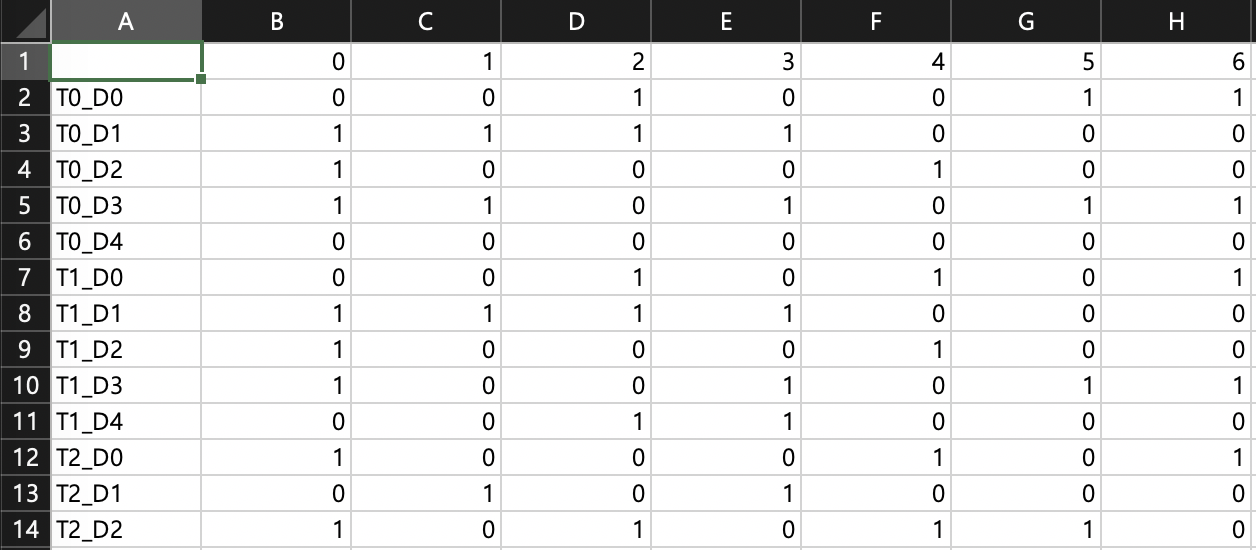
- avail.csv
결과
각 근무장소마다 알맞게 조교들이 배치되어 들어가있는 것을 볼 수 있다.
-
사무실

-
실험실
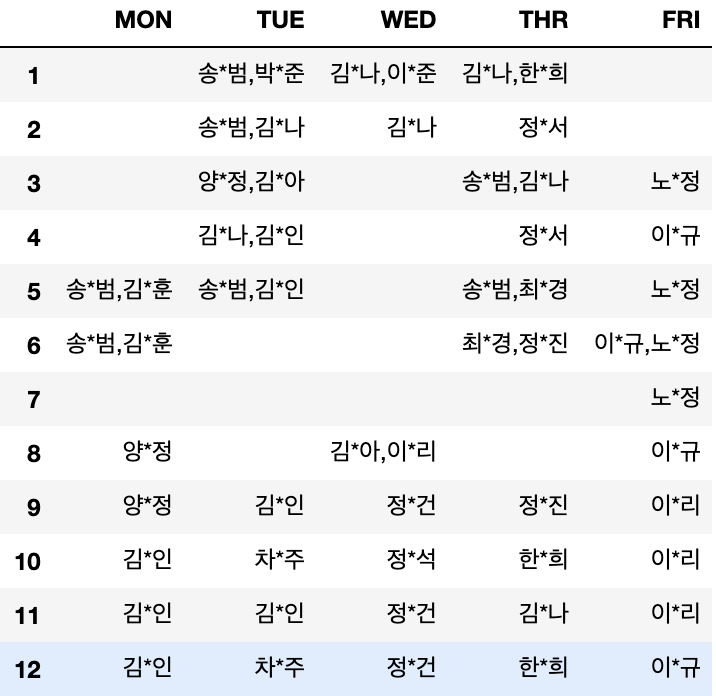
-
스터디룸
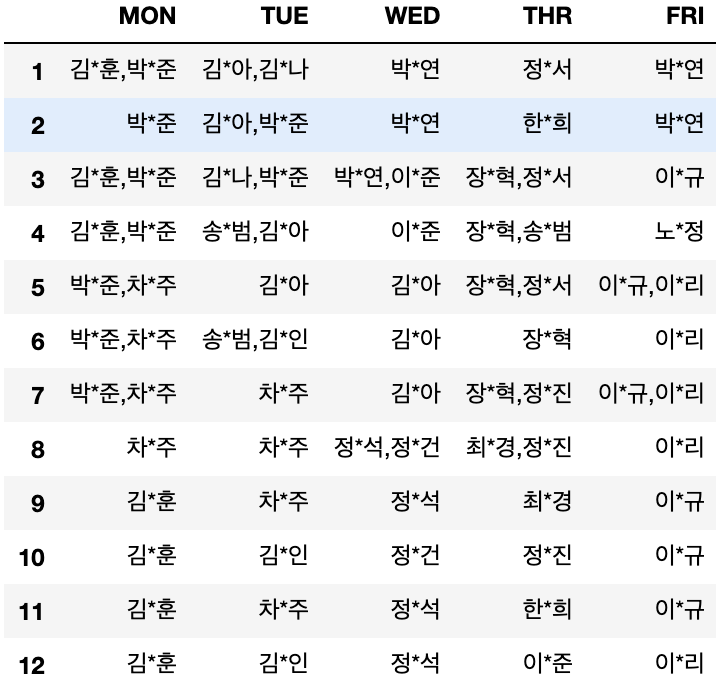
추후 업데이트
-
웹페이지나 프로그램을 통해 시스템화해서 매학기 사용할 수 있도록 한다.
-
각 학생들에게 각 가능한 시간에 선호도를 매기도록 한 후, 목적식에서 전체 학생들의 만족도를 최대화 시키는 방향으로 업그레이드