이번에는 dot product에 대해서 알아보자. 아래 내용은 유투버 쑤튜브님의 선형대수학 강의를 정리한 것이다.
dot product(scalar product)란?
dot product는 두 벡터를 곱해서 하나의 스칼라값이 나오도록 하는 연산이다.
\(v_1 = (x_1, y_1), v_2 = (x_2, y_2)\)를 서로 다른 벡터라고 했을 때, dot product연산은 다음과 같다.
\[v_1 \cdot v_2 = x_1 \cdot x_2 + y_1 \cdot y_2\]dot product와 norm
벡터 \(v\)에 대해 자기 자신을 dot product하면 다음과 같다.
\[v \cdot v = v_1 \cdot v_1 + v_2 \cdot v_2\]여기에 루트를 취하게 되면 다음과 같다.
\[\eqalignno{ \sqrt{v \cdot v} &= \sqrt{v_1 \cdot v_1 + v_2 \cdot v_2}\\ &= \lVert v \rVert }\]즉, norm은 dot product에 루트를 취한 것과 같다.
dot product의 기본성질
-
교환법칙이 성립한다.
-
분배법칙이 성립한다.
-
스칼라배가 가능하다.
-
제곱하게 되면 0보다 크거나 같다.
dot product의 여러가지 성질
-
제 2 코사인 법칙
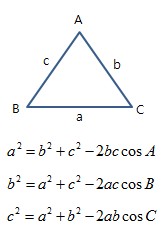
-
dot product의 기하학적 의미
두 벡터 \(u,v\)가 있고, \(u\)를 \(v\)에 대해 사영한 벡터를 \(w\)라고 할 때, \(u \cdot v\)는 \(\lVert w \rVert \lVert v \rVert\)와 같다.
그림으로 보면 다음과 같다.
하지만 이는 \(\theta\)가 0~90일 때 적용된다. 둔각이라면 -를 붙여줘야한다.
\[v_2 - v_1 = (x_2-x_1, y_2-y_1)\] \[\eqalignno{ cos\theta &= \frac{\lVert v_2 \rVert^2 \lVert v_1 \rVert^2 - \lVert v_2 - v_1 \rVert^2}{2\lVert v_2 \rVert \lVert v_1 \rVert} }\] \[\eqalignno{ \lVert v_2 \rVert^2 \lVert v_1 \rVert^2 - \lVert v_2 - v_1 \rVert^2 &= (\sqrt{v_2 \cdot v_2})^2 +(\sqrt{v_1 \cdot v_1})^2 - (\sqrt{(v_2-v_1) \cdot (v_2-v_1)})^2 \\ &= v_2 \cdot v_2 + v_1 \cdot v_1 - (v_2 - v_1) \cdot (v_2 - v_1) \\ &= v_2 \cdot v_2 + v_1 \cdot v_1 - \{ v_2 \cdot v_2 - v_1 \cdot v_1 - v_2 \cdot v_1 + v_1 \cdot v_1 \} \\ &= v_2 \cdot v_2 + v_1 \cdot v_1 - \{ v_2 \cdot v_2 + v_1 \cdot v_1 - 2v_1 \cdot v_2\} \\ &= 2v_1 \cdot v_2 }\] \[cos\theta = \frac{2v_1 \cdot v_2}{2\lVert v_1 \rVert \lVert v_2 \rVert} = \frac{v_1 \cdot v_2}{\lVert v_1 \rVert \lVert v_2 \rVert}\] \[v_1 \cdot v_2 = \lVert v_1 \rVert \lVert v_2 \rVert cos\theta\]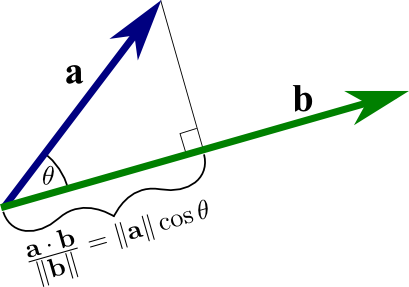
-
벡터의 projection(사영)
projection이란, 두 벡터가 있을 때, 한 벡터에 대해 수선을 내린 것을 의미한다.
아래 그림은 벡터 \(\vec{u}\)를 \(\vec{v}\)에 사영시킨 것을 보여준다.
그리고 이렇게 사영시킨 벡터를 \(proj_\vec{v}\vec{u}\)라고 표기한다.
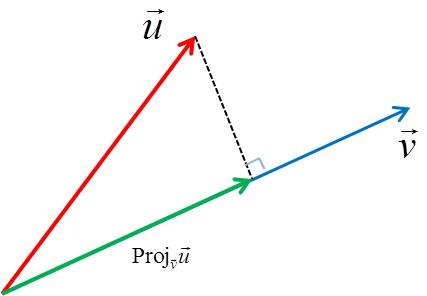
위에서 보았듯이, \(\vec{u} \cdot \vec{v}\)는 다음과 같다.
\[\vec{u} \cdot \vec{v} = \lVert proj_\vec{v}\vec{u} \rVert \lVert \vec{v} \rVert\]즉, \(proj_\vec{v}\vec{u}\)의 길이는 다음과 같다.
\[\lVert proj_\vec{v}\vec{u} \rVert = \frac{\vec{u} \cdot \vec{v}}{\lVert \vec{v} \rVert}\]여기에, \(proj_\vec{v}\vec{u}\)의 방향은 \(\vec{v}\)와 같기 때문에, \(vec{v}\)의 단위벡터를 곱하면 \(proj_\vec{v}\vec{u}\)를 알 수 있다.
\[\eqalignno{ proj_\vec{v}\vec{u} &= \frac{\vec{u} \cdot \vec{v}}{\lVert \vec{v} \rVert} \frac{v}{\lVert \vec{v} \rVert} \\ &= \frac{\vec{u} \cdot \vec{v}}{\lVert \vec{v} \rVert^2}\vec{v} \\ &= \frac{\vec{u} \cdot \vec{v}}{(\sqrt{\vec{v} \cdot \vec{v}})^2}\vec{v} \\ &= \frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}}\vec{v} }\] -
코시-슈바르츠 부등식(Cauchy-Schwarz Inequality)
\[(ax + by)^2 \leq (a^2+b^2)(x^2+y^2)\]여기서 \(ax+by\)는 dot product형태다.
\(u = (a,b), v = (x,y)\)라 할때 \(u \cdot v = ax + by\)이다.그리고 \(x^2 + y^2\)은 norm의 제곱과 같다. 즉, 위 식은 다음과 같다.
\[(u \cdot v)^2 \leq \lVert u \rVert^2 \lVert v\rVert^2\]이를 정리하면,
\[\lvert u \cdot v \rvert \leq \lVert u \rVert \lVert v\rVert\]이를 dot product의 성질을 이용해 간단히 증명해보자.
앞서 보았듯이, \(u \cdot v = \lVert u \rVert \lVert v \rVert cos\theta\)이 성립하고, \(-1 \leq cos\theta \leq 1\)이기 때문에 \(-\lVert u \rVert \lVert v \rVert \leq u\cdot v \leq \lVert u \rVert \lVert v \rVert\)이다. 이로써 \(\lvert u \cdot v \rvert \leq \lVert u \rVert \lVert v\rVert\)임을 알 수 있다. -
이와 비슷한 방식으로 dot product를 활용하여 삼각부등식(Triangle Inequality)나 피타고라스 정리 등을 증명할 수 있다.