선형대수의 기본으로, 먼저 벡터가 무엇인지에 대해서 알아보았다. 아래 내용은 유투버 쑤튜브님의 선형대수학 강의를 정리한 것이다.
벡터란 무엇인가?
다룰 수 있는 물리량에는 스칼라(scalar)와 벡터(vecter)가 있다.
- 스칼라 : 크기
- 벡터 : 크기 + 방향
벡터는 방향에 대한 정보도 담기 위해서 필요하다.
벡터 표현법
-
그림
화살표로 방향을, 화살표의 길이로 힘을 나타낸다.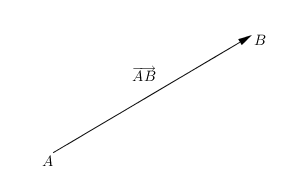
-
기호
위 그림과 같이, 시작점이 A이고 끝점이 B인 벡터의 크기는 \(\vec{AB}\)라고 표기한다.이때 \(\vec{AB} \neq \vec{BA}\)
벡터가 같기 위해서는?
방향과 크기가 모두 같아야 한다. -
좌표평면
그리고 벡터는 다음과 같이 좌표평면 위에 나타낼 수 있다.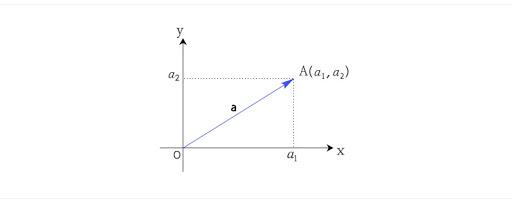
이때, 벡터의 시작점은 원점으로 한다.
이를 통해 벡터의 유일성이 보장된다.
그리고 끝점으로 벡터를 표현할 수 있게 된다. 이를 위치벡터라고 한다.만약 두개의 점이 각각 \(p_1=(x_1, y_1), p_2=(x_2, y_2)\)라고 정의되었을 때, 위치벡터는 \(\vec{p_1p_2} = (x_2-x_1,y_2-y_1)\)으로 정의될 수 있다.
- 위치벡터의 연산
- 덧셈 : 각각의 좌표를 더해주기만 하면 된다.
- 뺄셈 : 각각의 좌표를 빼준다.
- 스칼라배 : 각각의 좌표에 스칼라를 곱해준다.
- 위치벡터의 연산
벡터의 연산
-
덧셈
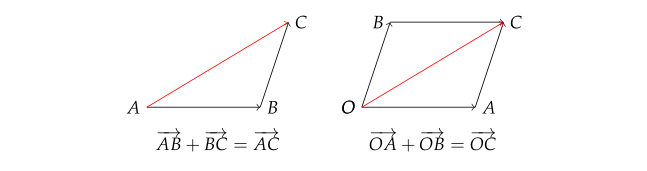
위 그림과 같이, 두개의 벡터를 더해줄 수 있다.
이는 평행사변형과 같은 모습을 하고 있기 때문에 평행사변형 법이라고 한다.그리고 벡터에 대해서는 교환법칙이 성립한다.
\[\vec{AB} + \vec{BA} = \vec{BA} + \vec{AB}\]
-
뺄셈
\(\vec{U} - \vec{V}\)뺄셈에 대해서는 위 그림과 같이 해줄 수 있다.
첫번째 그림과 같이 \(V\)의 끝점에서 \(U\)의 끝점으로 오는 삼각형 법과
두번째 그림과 같이 \(-V\)를 더하는 방식으로, 평행사변형 법을 이용하는 방법이 있다.뺄셈의 경우에는 교환법칙이 성립하지 않는다. 대신, 다음 식이 성립한다.
\[\vec{AB} - \vec{BA} = -(\vec{BA} - \vec{AB})\]
-
스칼라배(scalr multiplication)
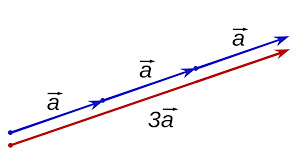
벡터의 스칼라배란, 벡터에 어떠한 스칼라 값을 곱하는 것인데, 이는 위 그림으로 이해할 수 있다.
